题目内容
13.已知a2+2a-3=0,求分式($\frac{a-2}{{a}^{2}+2a}$-$\frac{a-1}{{a}^{2}+4a+4}$)÷$\frac{a-4}{a+2}$的值.分析 先根据分式混合运算的法则把原式进行化简,再根据题意得出a2+2a=3代入原式进行计算即可.
解答 解:原式=($\frac{a-2}{a(a+2)}$-$\frac{a-1}{(a+2)^{2}}$)•$\frac{a+2}{a-4}$
=$\frac{(a+2)(a-2)-a(a-1)}{{a(a+2)}^{2}}$•$\frac{a+2}{a-4}$
=$\frac{{a}^{2}-4-{a}^{2}+a}{{a(a+2)}^{2}}$•$\frac{a+2}{a-4}$
=$\frac{a-4}{{a(a+2)}^{2}}$•$\frac{a+2}{a-4}$
=$\frac{1}{{a}^{2}+2a}$,
∵a2+2a-3=0,
∴a2+2a=3,
∴原式=$\frac{1}{3}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.下列英文字母是中心对称图形,但不是轴对称图形的是( )
| A. | N | B. | D | C. | W | D. | O |
18.一种细胞的直径约为1.6×10-6米,那么它的一百万倍相当于( )
| A. | 一元硬币的直径 | B. | 数学课本宽度 | ||
| C. | 五层楼房的高度 | D. | 初中学生小丽的身高 |
 如图,把边长为a+b的正方形分割成两个边长分别为a、b的小正方形及两个长方形(a≠b),若设两个小正方形的面积之和为A,两个长方形的面积之和为B,请比较A与B的大小,用含有a、b的代数式来说明理由.
如图,把边长为a+b的正方形分割成两个边长分别为a、b的小正方形及两个长方形(a≠b),若设两个小正方形的面积之和为A,两个长方形的面积之和为B,请比较A与B的大小,用含有a、b的代数式来说明理由.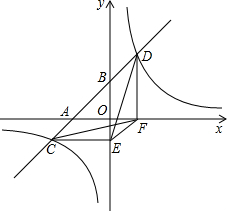 如图,一次函数y=ax+b的图象与x轴,y轴交于A,B两点,与反比例函数y=$\frac{k}{x}$的图象相交于C,D两点,分别过C,D两点作轴,轴的垂线,垂足为E,F,连结CF,DE,有下列结论:
如图,一次函数y=ax+b的图象与x轴,y轴交于A,B两点,与反比例函数y=$\frac{k}{x}$的图象相交于C,D两点,分别过C,D两点作轴,轴的垂线,垂足为E,F,连结CF,DE,有下列结论: 如图,在△ABC中,AB=AC,且D为BC上一点,CD=AD,AB=BD,则∠B的度数为36°.
如图,在△ABC中,AB=AC,且D为BC上一点,CD=AD,AB=BD,则∠B的度数为36°.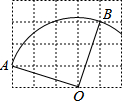 如图,扇形OAB是一个圆锥的侧面展开图,若小正方形方格的边长为1,则这个圆锥的底面半径为$\frac{\sqrt{10}}{4}$.
如图,扇形OAB是一个圆锥的侧面展开图,若小正方形方格的边长为1,则这个圆锥的底面半径为$\frac{\sqrt{10}}{4}$.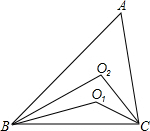 如图,△ABC中,∠A=60°,BO1、BO2三等分∠ABC,CO1、CO2三等分∠ACB.
如图,△ABC中,∠A=60°,BO1、BO2三等分∠ABC,CO1、CO2三等分∠ACB.