题目内容
15.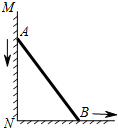 如图,一根长为5米的竹竿AB斜立于墙MN的右侧,底端B与墙角N 的距离为3米,当竹竿顶端A下滑x米时,底端B便随着向右滑行y米,反映y与x变化关系的大致图象是( )
如图,一根长为5米的竹竿AB斜立于墙MN的右侧,底端B与墙角N 的距离为3米,当竹竿顶端A下滑x米时,底端B便随着向右滑行y米,反映y与x变化关系的大致图象是( )| A. | 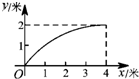 | B. | 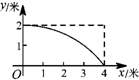 | C. | 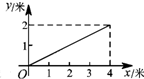 | D. | 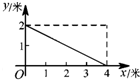 |
分析 在直角三角形ABN中,利用勾股定理求出AN的长,进而表示出A点下滑时AN与NB的长,确定出y与x的关系式,即可做出判断.
解答 解:在Rt△ABN中,AB=5米,NB=3米,
根据勾股定理得:AN=$\sqrt{A{B}^{2}-N{B}^{2}}$=4米,
若A下滑x米,AN=(4-x)米,
根据勾股定理得:NB=$\sqrt{{5}^{2}-(4-x)^{2}}$=3+y,
整理得:y=$\sqrt{25-(4-x)^{2}}$-3,
当x=0时,y=0;当x=4时,y=2,且不是直线变化的,
故选A.
点评 此题考查了动点问题的函数图象,解决本题的关键是读懂图意,列出y与x的函数解析式.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
15.从长度分别为1、3、5、7的四条线段中任选三条作边,能构成三角形的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
10.高速公路上,从3千米处开始,每隔4千米经过一个限速标志牌,并且从10千米处开始,每隔9千米经过一个速度监控仪,司机小王刚好在19千米的A处第一次同时经过这两种设施,那么,司机小王第二次同时经过这两种设施需要从A处继续行驶( )千米.
| A. | 36 | B. | 37 | C. | 55 | D. | 91 |
 如图,把边长为a+b的正方形分割成两个边长分别为a、b的小正方形及两个长方形(a≠b),若设两个小正方形的面积之和为A,两个长方形的面积之和为B,请比较A与B的大小,用含有a、b的代数式来说明理由.
如图,把边长为a+b的正方形分割成两个边长分别为a、b的小正方形及两个长方形(a≠b),若设两个小正方形的面积之和为A,两个长方形的面积之和为B,请比较A与B的大小,用含有a、b的代数式来说明理由. 在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得道△BAE,连接ED,若BC=5,BD=4,则以下四个结论中:①△BDE是等边三角形;②AE∥BC;③△ADE的周长是9;④∠ADE=∠BDC.其中正确的序号是( )
在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得道△BAE,连接ED,若BC=5,BD=4,则以下四个结论中:①△BDE是等边三角形;②AE∥BC;③△ADE的周长是9;④∠ADE=∠BDC.其中正确的序号是( )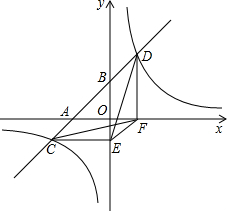 如图,一次函数y=ax+b的图象与x轴,y轴交于A,B两点,与反比例函数y=$\frac{k}{x}$的图象相交于C,D两点,分别过C,D两点作轴,轴的垂线,垂足为E,F,连结CF,DE,有下列结论:
如图,一次函数y=ax+b的图象与x轴,y轴交于A,B两点,与反比例函数y=$\frac{k}{x}$的图象相交于C,D两点,分别过C,D两点作轴,轴的垂线,垂足为E,F,连结CF,DE,有下列结论: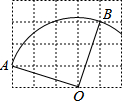 如图,扇形OAB是一个圆锥的侧面展开图,若小正方形方格的边长为1,则这个圆锥的底面半径为$\frac{\sqrt{10}}{4}$.
如图,扇形OAB是一个圆锥的侧面展开图,若小正方形方格的边长为1,则这个圆锥的底面半径为$\frac{\sqrt{10}}{4}$.