题目内容
9.已知关于x的方程|x|-|x-1|=a恰好只有一个实数解,则实数a的取值范围为-1<a≤1.分析 分成x≤0,0<x≤1和x>1三种情况进行讨论,去掉绝对值符号即可判断.
解答 解:当x≤0时,原式即-x-(1-x)=a,
即-1=a,此时x有无数个解;
当0<x≤1时,原式即x-(1-x)=a,
即2x-1=a,
则x=$\frac{a+1}{2}$,
根据题意得0<$\frac{a+1}{2}$≤1,
解得-1<a≤1;
当x>1时,原式即x-(x-1)=a,此时x有无数个解.
总之a的范围是-1<a≤1.
点评 本题考查一元一次方程的解,正确根据绝对值的性质进行讨论是关键.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
20.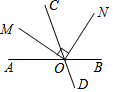 如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM.若∠AOC=70°,则∠CON的度数为( )
如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM.若∠AOC=70°,则∠CON的度数为( )
 如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM.若∠AOC=70°,则∠CON的度数为( )
如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM.若∠AOC=70°,则∠CON的度数为( )| A. | 65° | B. | 55° | C. | 45° | D. | 35° |
17.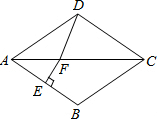 如图,在菱形ABCD中,∠BAD=70°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于( )
如图,在菱形ABCD中,∠BAD=70°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于( )
 如图,在菱形ABCD中,∠BAD=70°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于( )
如图,在菱形ABCD中,∠BAD=70°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于( )| A. | 55° | B. | 65° | C. | 75° | D. | 85° |
14.下列运算正确的是( )
| A. | a2•a3=a6 | B. | (-2ab3)2=-4a2b6 | C. | (-a2)3=-a6 | D. | 2a+3b=5ab |
19. 如图,这是2016年12月的日历表,任意圈出一竖列上相邻的四个数,请你运用方程的思想来研究,发现这四个数的和不可能是( )
如图,这是2016年12月的日历表,任意圈出一竖列上相邻的四个数,请你运用方程的思想来研究,发现这四个数的和不可能是( )
 如图,这是2016年12月的日历表,任意圈出一竖列上相邻的四个数,请你运用方程的思想来研究,发现这四个数的和不可能是( )
如图,这是2016年12月的日历表,任意圈出一竖列上相邻的四个数,请你运用方程的思想来研究,发现这四个数的和不可能是( )| A. | 50 | B. | 58 | C. | 68 | D. | 70 |