题目内容
17.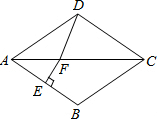 如图,在菱形ABCD中,∠BAD=70°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于( )
如图,在菱形ABCD中,∠BAD=70°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于( )| A. | 55° | B. | 65° | C. | 75° | D. | 85° |
分析 如图,连接BF,想办法求出∠CBF=75°,再证明△BCF≌△DCF(SAS),即可解决问题.
解答 解:如图,连接BF,
在菱形ABCD中,∠BAC=$\frac{1}{2}$∠BAD=$\frac{1}{2}$×70°=35°,∠BCF=∠DCF,BC=DC,
∠ABC=180°-∠BAD=180°-70°=110°,
∵EF是线段AB的垂直平分线,
∴AF=BF,∠ABF=∠BAC=35°,
∴∠CBF=∠ABC-∠ABF=110°-35°=75°,
∵在△BCF和△DCF中,
$\left\{\begin{array}{l}{BC=DC}\\{∠BCF=∠DCF}\\{CF=CF}\end{array}\right.$,
∴△BCF≌△DCF(SAS),
∴∠CDF=∠CBF=75°,
故选C.
点评 本题考查了菱形的性质,全等三角形的判定与性质,线段垂直平分线上的点到线段两端点的距离相等的性质,解题的关键是学会用转化的思想思考问题,属于中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.下列计算中,错误的是( )
| A. | -3a+2a=-a | B. | a3•a2=a6 | C. | (3a3)2=9a6 | D. | 6a2b÷3b=2a2 |
6.下列方程是一元二次方程的是( )
| A. | 9x2-5x=9 | B. | 4x+8=0 | C. | 6x3+8x-1=0 | D. | x2-$\frac{1}{x}$=6 |
7. 如图,AB为⊙O的切线,A为切点,BO的延长线交⊙O于点C,∠OAC=35°,则∠B的度数是( )
如图,AB为⊙O的切线,A为切点,BO的延长线交⊙O于点C,∠OAC=35°,则∠B的度数是( )
 如图,AB为⊙O的切线,A为切点,BO的延长线交⊙O于点C,∠OAC=35°,则∠B的度数是( )
如图,AB为⊙O的切线,A为切点,BO的延长线交⊙O于点C,∠OAC=35°,则∠B的度数是( )| A. | 15° | B. | 20° | C. | 25° | D. | 35° |
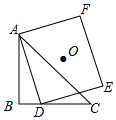 如图,△ABC中,∠ABC=90°,AB=BC=4,D为BC边上一动点,点O是正方形ADEF的中心,当点D沿BC边从点B运动到点C时,点O运动的路径长为2$\sqrt{2}$.
如图,△ABC中,∠ABC=90°,AB=BC=4,D为BC边上一动点,点O是正方形ADEF的中心,当点D沿BC边从点B运动到点C时,点O运动的路径长为2$\sqrt{2}$. 如图,⊙A、⊙B、⊙C两两不相交,且半径都是2cm,则图中三个扇形(阴影部分)的面积之和是10πcm2.
如图,⊙A、⊙B、⊙C两两不相交,且半径都是2cm,则图中三个扇形(阴影部分)的面积之和是10πcm2.