题目内容
1.已知一个圆锥形零件的高线长为4,底面半径为3,则这个圆锥形的零件的侧面积为15π.分析 首先利用勾股定理计算出母线长,再利用圆锥的侧面积公式S=πrl得出圆锥侧面积.
解答 解:∵高线长为4,底面半径为3,
∴母线长为:$\sqrt{{4}^{2}+{3}^{2}}$=5,
∴圆锥侧面积公式为:S=πrl=π×5×3=15π,
故答案为:15π.
点评 此题主要考查了圆锥的侧面积公式,关键是计算出圆锥的母线长.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
11.下列等式一定成立的是( )
| A. | 2a+3b=5ab | B. | (a3)2=a5 | C. | a2•a3=a5 | D. | (a+b)2=a2+b2 |
12.下列计算中,错误的是( )
| A. | -3a+2a=-a | B. | a3•a2=a6 | C. | (3a3)2=9a6 | D. | 6a2b÷3b=2a2 |
6.下列方程是一元二次方程的是( )
| A. | 9x2-5x=9 | B. | 4x+8=0 | C. | 6x3+8x-1=0 | D. | x2-$\frac{1}{x}$=6 |
13.要使代数式$\frac{\sqrt{x+1}}{x}$有意义,则实数x的取值范围是( )
| A. | x≥1 | B. | x≥-1 | C. | x≥-1且x≠0 | D. | x>-1且x≠0 |
10.-3的相反数是( )
| A. | -3 | B. | 3 | C. | $\frac{1}{3}$ | D. | $-\frac{1}{3}$ |
 如图所示的几何体是由五个小正方体组合而成的,则它的左视图是( )
如图所示的几何体是由五个小正方体组合而成的,则它的左视图是( )



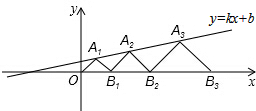 如图,在平面直角坐标系xOy中,点A1,A2,A3,…和B1,B2,B3,…分别在直线y=kx+b和x轴上,△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形,如果A1(1,1),A2($\frac{7}{2}$,$\frac{3}{2}$),那么点A3的纵坐标是$\frac{9}{4}$,点An的纵坐标是($\frac{3}{2}$)n-1.
如图,在平面直角坐标系xOy中,点A1,A2,A3,…和B1,B2,B3,…分别在直线y=kx+b和x轴上,△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形,如果A1(1,1),A2($\frac{7}{2}$,$\frac{3}{2}$),那么点A3的纵坐标是$\frac{9}{4}$,点An的纵坐标是($\frac{3}{2}$)n-1.