题目内容
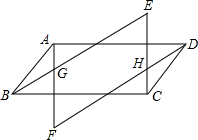 如图,四边形ABCD是平行四边形,作AF∥CE,BE∥DF,AF交BE于G点,交DF于F点,CE交DF于H点、交BE于E点.
如图,四边形ABCD是平行四边形,作AF∥CE,BE∥DF,AF交BE于G点,交DF于F点,CE交DF于H点、交BE于E点.求证:△EBC≌△FDA.
考点:平行四边形的性质,全等三角形的判定
专题:证明题
分析:根据平行三边的性质可知:AD=BC,由平行四边形的判定方法易证四边形BMDK和四边形AJCN是平行四边形,所以得∠FAD=∠ECB,∠ADF=∠EBC,进而证明:△EBC≌△FDA.
解答: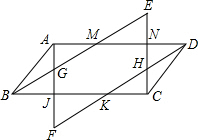 证明:∵四边形ABCD是平行四边形,
证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵AF∥CE,BE∥DF,
∴四边形BMDK和四边形AJCN是平行四边形,
∴∠FAD=∠ECB,∠ADF=∠EBC,
在△EBC和△FDA中,
∴△EBC≌△FDA(ASA).
 证明:∵四边形ABCD是平行四边形,
证明:∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,
∵AF∥CE,BE∥DF,
∴四边形BMDK和四边形AJCN是平行四边形,
∴∠FAD=∠ECB,∠ADF=∠EBC,
在△EBC和△FDA中,
|
∴△EBC≌△FDA(ASA).
点评:本题考查了平行四边形的判定以及全等三角形的判定,在全等三角形的5种判定方法中,选用哪一种方法,取决于题目中的已知条件,若已知两边对应相等,则找它们的夹角或第三边;若已知两角对应相等,则必须再找一组对边对应相等,且要是两角的夹边,若已知一边一角,则找另一组角,或找这个角的另一组对应邻边.

练习册系列答案
相关题目
 如图,已知:△ABC中,AB=AC,M是BC的中点,D、E分别是AB、AC边上的点,且BD=CE.求证:MD=ME.
如图,已知:△ABC中,AB=AC,M是BC的中点,D、E分别是AB、AC边上的点,且BD=CE.求证:MD=ME.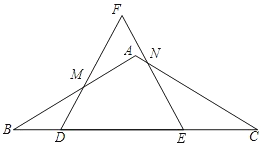 如图,在△ABC中,AB=AC,∠B=30°,BC=8,D在边BC上,E在线段DC上,DE=4,△DEF是等边三角形,边DF交边AB于点M,边EF交边AC于点N.
如图,在△ABC中,AB=AC,∠B=30°,BC=8,D在边BC上,E在线段DC上,DE=4,△DEF是等边三角形,边DF交边AB于点M,边EF交边AC于点N.
 如图,一艘轮船以30海里/小时的速度由西向东航行,途中接到台风警报,台风中心正以60海里/小时的速度由南向北移动,距台风中心20海里的圆形区域(包括边界)都属于台风区,当轮船到A处时,测得台风中心移到位于点A正南方向的B处,且AB=40海里.
如图,一艘轮船以30海里/小时的速度由西向东航行,途中接到台风警报,台风中心正以60海里/小时的速度由南向北移动,距台风中心20海里的圆形区域(包括边界)都属于台风区,当轮船到A处时,测得台风中心移到位于点A正南方向的B处,且AB=40海里.