题目内容
 如图,一艘轮船以30海里/小时的速度由西向东航行,途中接到台风警报,台风中心正以60海里/小时的速度由南向北移动,距台风中心20海里的圆形区域(包括边界)都属于台风区,当轮船到A处时,测得台风中心移到位于点A正南方向的B处,且AB=40海里.
如图,一艘轮船以30海里/小时的速度由西向东航行,途中接到台风警报,台风中心正以60海里/小时的速度由南向北移动,距台风中心20海里的圆形区域(包括边界)都属于台风区,当轮船到A处时,测得台风中心移到位于点A正南方向的B处,且AB=40海里.(1)若轮船以原方向、原速度继续航行:
①船长发现,当台风中心到达A处时,轮船肯定受影响,为什么?
②求轮船从A点出发到最初遇到台风的时间;
(2)若轮船在A处迅速改变航线,向北偏东60°的方向的避风港以30海里/小时的速度驶去,轮船还会不会受到影响?若会,试求轮船最初遇到台风的时间;若不会,请说明理由.
考点:勾股定理的应用
专题:
分析:(1)①求出当台风中心到达A处时,所用时间,进而求出轮船此时驶离A处距离,比较即可;
②当轮船在t小时后到达A1时,最初遇到台风,此时台风中心到达B1,进而表示出各线段长,再利用勾股定理求出即可;
(2)当轮船在m时后到达A2时,最初遇到台风,此时台风中心到达B2,进而得出A2B2=20,A2A=30m,AB2=60m-40,
作A2E⊥AB2,垂足为E,则A2E=15
m,AE=15m,EB2=AE-AB2,再利用勾股定理求出即可.
②当轮船在t小时后到达A1时,最初遇到台风,此时台风中心到达B1,进而表示出各线段长,再利用勾股定理求出即可;
(2)当轮船在m时后到达A2时,最初遇到台风,此时台风中心到达B2,进而得出A2B2=20,A2A=30m,AB2=60m-40,
作A2E⊥AB2,垂足为E,则A2E=15
| 3 |
解答: 解:(1)①会受影响,
解:(1)①会受影响,
当台风中心到达A处时,用时:
=
(小时),
则轮船此时驶离A处:30×
=20(海里),因此轮船肯定受影响;
②如图1,若轮船在t小时后到达A1时,最初遇到台风,此时台风中心到达B1,
则A1B1=20海里,A1A=30t,AB1=40-60t,
由勾股定理知,(30t)2+(40-60t)2=202,
解得:t1=
,t2=
,
则轮船从A点出发到最初遇到台风的时间是
小时;
(2)会,
理由:如图2,若轮船在m时后到达A2时,最初遇到台风,此时台风中心到达B2,
则A2B2=20,A2A=30m,AB2=60m-40,
作A2E⊥AB2,垂足为E,
则A2E=30m×sin60°=15
m,AE=15m,EB2=AE-AB2=15m-(60m-40)=40-45m,
由勾股定理得:(15
m)2+(40-45m)2=202,
解得:m1=m2=
,
则轮船从A点出发到最初遇到台风的时间是
小时.
 解:(1)①会受影响,
解:(1)①会受影响,当台风中心到达A处时,用时:
| 40 |
| 60 |
| 2 |
| 3 |
则轮船此时驶离A处:30×
| 2 |
| 3 |
②如图1,若轮船在t小时后到达A1时,最初遇到台风,此时台风中心到达B1,
则A1B1=20海里,A1A=30t,AB1=40-60t,
由勾股定理知,(30t)2+(40-60t)2=202,
解得:t1=
| 2 |
| 3 |
| 2 |
| 5 |
则轮船从A点出发到最初遇到台风的时间是
| 2 |
| 5 |
(2)会,
理由:如图2,若轮船在m时后到达A2时,最初遇到台风,此时台风中心到达B2,
则A2B2=20,A2A=30m,AB2=60m-40,
作A2E⊥AB2,垂足为E,
则A2E=30m×sin60°=15
| 3 |
由勾股定理得:(15
| 3 |
解得:m1=m2=
| 2 |
| 3 |
则轮船从A点出发到最初遇到台风的时间是
| 2 |
| 3 |
点评:此题主要考查了勾股定理的应用以及锐角三角函数的应用,根据题意分别表示出各线段的长是解题关键.

练习册系列答案
相关题目
一个等腰三角形的两边长分别是3和7,则它的周长为( )
| A、17 | B、15 |
| C、13 | D、13或17 |
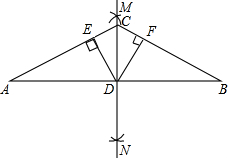 如图,分别以线段AB的两个端点为圆心,大于AB的长为半径作弧,两弧交于M、N两点,连接MN,交AB于点D、C是直线MN上任意一点,连接CA、CB,过点D作DE⊥AC于点E,DF⊥BC于点F.
如图,分别以线段AB的两个端点为圆心,大于AB的长为半径作弧,两弧交于M、N两点,连接MN,交AB于点D、C是直线MN上任意一点,连接CA、CB,过点D作DE⊥AC于点E,DF⊥BC于点F.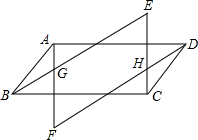 如图,四边形ABCD是平行四边形,作AF∥CE,BE∥DF,AF交BE于G点,交DF于F点,CE交DF于H点、交BE于E点.
如图,四边形ABCD是平行四边形,作AF∥CE,BE∥DF,AF交BE于G点,交DF于F点,CE交DF于H点、交BE于E点. 如图,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BC于点E.
如图,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BC于点E.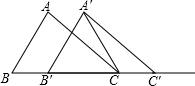 如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移2个单位后,得到△A′B′C′,连接A′C,则△A′B′C的周长为
如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移2个单位后,得到△A′B′C′,连接A′C,则△A′B′C的周长为