题目内容
如图，BC是⊙O的直径，A是圆上一点，AD⊥BC，垂足为点D．P为 |
| AC |
（1）当
|
| PA |
|
| AB |
（2）图中是否存在比例线段？找找看；
（3）当AF=AE时，点P在什么位置？
考点：圆周角定理,圆心角、弧、弦的关系,相似三角形的判定与性质
专题：
分析：（1）如图，作辅助线，证明
=
，即可解决问题；
（2）证明△APF∽△BCF，再利用射影定理即可找出图中的比例线段；
（3）可通过三角形的外角定理证明∠ABE=∠PAC，即可解决问题．
|
| BG |
|
| PA |
（2）证明△APF∽△BCF，再利用射影定理即可找出图中的比例线段；
（3）可通过三角形的外角定理证明∠ABE=∠PAC，即可解决问题．
解答：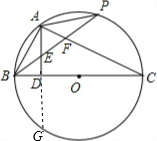
解：（1）AE=BE；
如图，延长AD，交⊙O于点G；
∵AD⊥BC，BC为⊙O的直径，
∴
=
，而
=
，
∴
=
，
∴∠BAE=∠ABE，
∴AE=BE．
（2）图中存在比例线段，
∵∠P=∠C，∠PAF=∠CBF，
∴△APF∽△BCF，
∴
=
=
；
由射影定理得：
AB2=BD•BC，AC2=DC•BC，AC2=DC•BC．
（3）当AE=AF时，点P为
的中点．
解：（1）AE=BE；如图，延长AD，交⊙O于点G；
∵AD⊥BC，BC为⊙O的直径，
∴
|
| AB |
|
| BG |
|
| PA |
|
| AB |
∴
|
| BG |
|
| PA |
∴∠BAE=∠ABE，
∴AE=BE．
（2）图中存在比例线段，
∵∠P=∠C，∠PAF=∠CBF，
∴△APF∽△BCF，
∴
| AP |
| BC |
| AF |
| BF |
| PF |
| CF |
由射影定理得：
AB2=BD•BC，AC2=DC•BC，AC2=DC•BC．
（3）当AE=AF时，点P为
|
| AC |
点评：该命题以圆为载体，主要考查了垂径定理、射影定理、相似三角形的判定及其性质等几何知识点；对综合的分析问题解决问题的能力提出了较高的要求．
练习册系列答案
相关题目
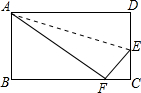折叠矩形纸片ABCD的一边AD，使点D落在BC边的点F处，已知AB=8cm，BC=10cm，折痕AE的长（ ）A、5
| ||
B、5
| ||
| C、12cm | ||
| D、13cm |
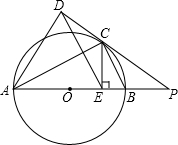PC切圆O于C，PBA为过圆心O的割线，点D在射线PC上，CE⊥AB于E，AC平分∠DAB，连接DE，CB，求证：DE∥BC．
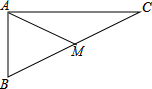如图，在△ABC中，∠ABC=90°，AB=4cm，AC=6cm，AM是中线．
已知正方形ABCD的边长是2，点E、F分别是BC、CD的中点，AE与BF交于点O．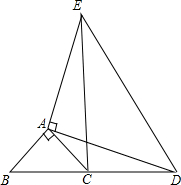
如图，△ABC和△ADE都是等腰三角形，AB=AC，AD=AE，且∠BAC=90°，∠DAE=90°，B，C，D在同一条直线上．则线段BD与CE有什么关系？请说明理由．
如图所示，用规格相同的正方形瓷砖铺成矩形地面，其中，横向瓷砖比纵向瓷砖每排多5块，矩形地面最外面一圈为灰色瓷砖，其余部分全为白色瓷砖．设纵向每排有n块瓷砖．