题目内容
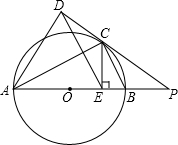 PC切圆O于C,PBA为过圆心O的割线,点D在射线PC上,CE⊥AB于E,AC平分∠DAB,连接DE,CB,求证:DE∥BC.
PC切圆O于C,PBA为过圆心O的割线,点D在射线PC上,CE⊥AB于E,AC平分∠DAB,连接DE,CB,求证:DE∥BC.考点:切线的性质
专题:证明题
分析:首先证明∠DCA=∠CBA;然后证明D、A、E、C四点共圆,进而得到∠DCA=∠DEA,问题即可解决.
解答: 证明:∵DC为⊙O的切线,
证明:∵DC为⊙O的切线,
∴∠DCA=∠CBA;
又∵AC平分∠DAB,
∴∠DAC=∠BAC,
∴△DAC∽△CAB,
∴∠ADC=∠ACB;
∵AB为⊙O的直径,
∴∠ADC=∠ACB=90°,
∵CE⊥AB,
∴∠ADC=∠AEC=90°,
∴∠ADC+∠AEC=180°,
∴D、A、E、C四点共圆,
∴∠DCA=∠DEA,
∴∠DEA=∠CBA,
∴DE∥BC.
 证明:∵DC为⊙O的切线,
证明:∵DC为⊙O的切线,∴∠DCA=∠CBA;
又∵AC平分∠DAB,
∴∠DAC=∠BAC,
∴△DAC∽△CAB,
∴∠ADC=∠ACB;
∵AB为⊙O的直径,
∴∠ADC=∠ACB=90°,
∵CE⊥AB,
∴∠ADC=∠AEC=90°,
∴∠ADC+∠AEC=180°,
∴D、A、E、C四点共圆,
∴∠DCA=∠DEA,
∴∠DEA=∠CBA,
∴DE∥BC.
点评:该命题以圆为载体,以切线性质的考查为切入点构造而成;综合考查了切线的性质、圆周角定理的推论、四点共圆的判定、平行线的判定等几何知识点;对综合的分析问题解决问题的能力提出了较高的要求.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
 已知一次函数y=-2x+3
已知一次函数y=-2x+3
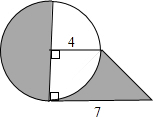 求阴影部分的面积:
求阴影部分的面积: 如图,BC是⊙O的直径,A是圆上一点,AD⊥BC,垂足为点D.P为
如图,BC是⊙O的直径,A是圆上一点,AD⊥BC,垂足为点D.P为
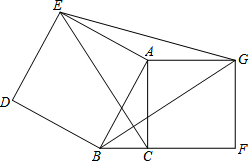 如图,在△ABC中,∠ACB=90°,分别以边AB、AC向外作正方形ABDE和正方形ACFG,连接CE,BG,EG.(正方形的各边都相等,各角均为90°)
如图,在△ABC中,∠ACB=90°,分别以边AB、AC向外作正方形ABDE和正方形ACFG,连接CE,BG,EG.(正方形的各边都相等,各角均为90°)