题目内容
如图所示，用规格相同的正方形瓷砖铺成矩形地面，其中，横向瓷砖比纵向瓷砖每排多5块，矩形地面最外面一圈为灰色瓷砖，其余部分全为白色瓷砖．设纵向每排有n块瓷砖．（1）设灰色瓷砖的总数为y块．
①用含n的代数式表示y，则y=
②y与n具有怎样的函数关系？
（2）设白色瓷砖的总数为z块．
①用含n的代数式表示z，则z=
②z是n的函数吗？说说理由．
考点：一次函数的应用,规律型：图形的变化类
专题：
分析：（1）根据白瓷砖的每行有（n+5-2）个，每列有（n-2）个，即可表示白瓷砖的数量，再让总数减去白瓷砖的数量即为灰色瓷砖的数量；
（2）根据白瓷砖的每行有（n+5-2）个，每列有（n-2）个，即可表示白瓷砖的数量，
（2）根据白瓷砖的每行有（n+5-2）个，每列有（n-2）个，即可表示白瓷砖的数量，
解答：解：（1）①需用白瓷砖（n-2）（n+5-2）块，则需要灰色瓷砖的数量是：n（n+5）-（n-2）（n+5-2）块，则
y=n（n+5）-（n-2）（n+5-2）=
故答案是：-6n+6；
②由①知，y=-6n+6，则y与n是一次函数关系；
（2）①白瓷砖的每行有（n+5-2）个，每列有（n-2）个，则白瓷砖的数量是：（n-2）（n+5-2）．依题意得
z=（n-2）（n+5-2）=n2+n-6．
故答案是：n2+n-6；
②由①知：则z=n2+n-6，在z与n是二次函数关系．
y=n（n+5）-（n-2）（n+5-2）=
故答案是：-6n+6；
②由①知，y=-6n+6，则y与n是一次函数关系；
（2）①白瓷砖的每行有（n+5-2）个，每列有（n-2）个，则白瓷砖的数量是：（n-2）（n+5-2）．依题意得
z=（n-2）（n+5-2）=n2+n-6．
故答案是：n2+n-6；
②由①知：则z=n2+n-6，在z与n是二次函数关系．
点评：考查了一次函数的应用和规律型：图形的变化类．解决此题的关键是能够正确结合图形用代数式表示出灰色、白瓷砖的数量，再根据题意列方程求解．
练习册系列答案
相关题目
已知一次函数y=-2x+3
如图，BC是⊙O的直径，A是圆上一点，AD⊥BC，垂足为点D．P为
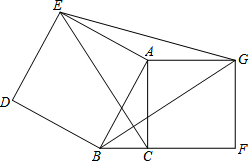如图，在△ABC中，∠ACB=90°，分别以边AB、AC向外作正方形ABDE和正方形ACFG，连接CE，BG，EG．（正方形的各边都相等，各角均为90°）