题目内容
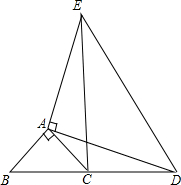 如图,△ABC和△ADE都是等腰三角形,AB=AC,AD=AE,且∠BAC=90°,∠DAE=90°,B,C,D在同一条直线上.则线段BD与CE有什么关系?请说明理由.
如图,△ABC和△ADE都是等腰三角形,AB=AC,AD=AE,且∠BAC=90°,∠DAE=90°,B,C,D在同一条直线上.则线段BD与CE有什么关系?请说明理由.考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:易证∠CAE=∠BAD,可得△BAD≌△CAE,根据全等三角形对应边相等的性质可得BD=CE.
解答:解:BD=CE,
证明:∵∠BAC=∠DAE=90°,
∴∠CAE=∠BAD=90°+∠CAD,
在△BAD和△CAE中,
,
∴△BAD≌△CAE,(SAS),
∴BD=CE.
证明:∵∠BAC=∠DAE=90°,
∴∠CAE=∠BAD=90°+∠CAD,
在△BAD和△CAE中,
|
∴△BAD≌△CAE,(SAS),
∴BD=CE.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△BAD≌△CAE是解题的关键.

练习册系列答案
相关题目
若x2-y2=3,则(x+y)2(x-y)2的值是( )
| A、3 | B、6 | C、9 | D、18 |
 如下图,D是△ABC的边BC的中点,且
如下图,D是△ABC的边BC的中点,且| AE |
| BE |
| 1 |
| 3 |
| AF |
| FC |
A、
| ||
B、
| ||
C、
| ||
D、
|
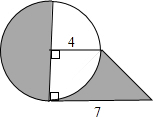 求阴影部分的面积:
求阴影部分的面积: 如图,BC是⊙O的直径,A是圆上一点,AD⊥BC,垂足为点D.P为
如图,BC是⊙O的直径,A是圆上一点,AD⊥BC,垂足为点D.P为
 如图所示,在等腰△ABC中,∠C=90°,AC=BC,BE=ED=CF,求∠CEF+∠CAD.
如图所示,在等腰△ABC中,∠C=90°,AC=BC,BE=ED=CF,求∠CEF+∠CAD.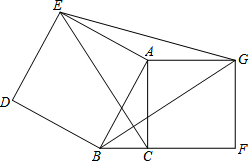 如图,在△ABC中,∠ACB=90°,分别以边AB、AC向外作正方形ABDE和正方形ACFG,连接CE,BG,EG.(正方形的各边都相等,各角均为90°)
如图,在△ABC中,∠ACB=90°,分别以边AB、AC向外作正方形ABDE和正方形ACFG,连接CE,BG,EG.(正方形的各边都相等,各角均为90°)