题目内容
18. 如图,在△ABC中,∠BAC=45°,AB=4cm,将△ABC绕点B按逆时针方向旋转45°后得到△A′BC′,则阴影部分的面积为( )cm2.
如图,在△ABC中,∠BAC=45°,AB=4cm,将△ABC绕点B按逆时针方向旋转45°后得到△A′BC′,则阴影部分的面积为( )cm2.| A. | 8$\sqrt{2}$ | B. | 4$\sqrt{3}$ | C. | 8$\sqrt{3}$ | D. | 4$\sqrt{2}$ |
分析 根据旋转的性质得∠ABA′=45°,BA′BA=4,△ABC≌△A′BC′,则S△ABC=S△A′BC′,再利用面积的和差可得S阴影部分=S△ABA′,接着证明△ADB为等腰直角三角形,得到∠ADB=90°,AD=2$\sqrt{2}$,然后利用三角形面积公式计算S△ABA,从而得到S阴影部分.
解答 解: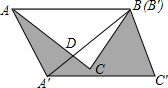 AC与BA′相交于D,如图所示,
AC与BA′相交于D,如图所示,
∵△ABC绕点B按逆时针方向旋转45°后得到△A′BC′,
∴∠ABA′=45°,BA′=BA=4,△ABC≌△A′BC′,
∴S△ABC=S△A′BC′,
∵S四边形AA′C′B=S△ABC+S阴影部分=S△A′BC′+S△ABA′,
∴S阴影部分=S△ABA′,
∵∠BAC=45°,
∴△ADB为等腰直角三角形,
∴∠ADB=90°,AD=$\frac{\sqrt{2}}{2}$AB=2$\sqrt{2}$,
∴S△ABA′=$\frac{1}{2}$AD•BA′=$\frac{1}{2}$×2$\sqrt{2}$×4=4$\sqrt{2}$(cm2),
∴S阴影部分=4$\sqrt{2}$cm2.
故选:D.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰直角三角形的性质.运用面积的和差解决不规则图形的面积是解决此题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
13.若a、b为实数,且满足$|{a-2}|+\sqrt{3-b}=0$,则b-a的值为( )
| A. | 1 | B. | 0 | C. | -1 | D. | 以上都不对 |
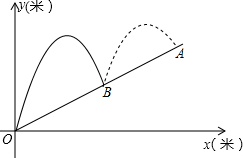 如图,小张在山坡下点O向山上球洞A打高尔夫球,球的运行高度y(m)与运行的水平距离x(m)都满足y=-$\frac{1}{4}$(x+h)2+9(山坡看作一条直线),山坡上的各点的纵坐标与横坐标比是1:2,第一杆球落在B处(O、B、A在一条直线上)
如图,小张在山坡下点O向山上球洞A打高尔夫球,球的运行高度y(m)与运行的水平距离x(m)都满足y=-$\frac{1}{4}$(x+h)2+9(山坡看作一条直线),山坡上的各点的纵坐标与横坐标比是1:2,第一杆球落在B处(O、B、A在一条直线上)