题目内容
7.计算:(1)$\frac{2x-6}{4-4x+{x}^{2}}$÷(x+3)$•\frac{{x}^{2}+x-6}{3-x}$
(2)(-$\frac{b}{a}$)2•(-$\frac{a}{{b}^{2}}$)3÷(-$\frac{b}{a}$)4
(3)(4nm-3)-2÷(-$\frac{1}{2}$m2n)-3
(4)($\frac{4{x}^{3}-2{x}^{2}}{2{x}^{2}+x-1}$$-\frac{3{x}^{3}}{x+1}$)÷(1-$\frac{x}{x+1}$)÷x2.
分析 (1)将除法变为乘法,再因式分解和约分即可求解;
(2)将除法变为乘法,再约分即可求解;
(3)先计算积的乘方,再将除法变为乘法,约分计算即可求解;
(4)先通分计算小括号里面的减法,再将除法变为乘法,再约分即可求解.
解答 解:(1)$\frac{2x-6}{4-4x+{x}^{2}}$÷(x+3)$•\frac{{x}^{2}+x-6}{3-x}$
=$\frac{2(x-3)}{(x-2)^{2}}$•$\frac{1}{x+3}$•$\frac{(x+3)(x-2)}{-(x-3)}$
=$\frac{-2}{x-2}$;
(2)(-$\frac{b}{a}$)2•(-$\frac{a}{{b}^{2}}$)3÷(-$\frac{b}{a}$)4
=$\frac{{b}^{2}}{{a}^{2}}$•(-$\frac{{a}^{3}}{{b}^{6}}$)•$\frac{{a}^{4}}{{b}^{4}}$
=--$\frac{{a}^{5}}{{b}^{8}}$;
(3)(4nm-3)-2÷(-$\frac{1}{2}$m2n)-3
=$\frac{{m}^{6}}{16{n}^{2}}$•$\frac{-{n}^{3}}{8{m}^{6}}$
=-$\frac{n}{128}$;
(4)($\frac{4{x}^{3}-2{x}^{2}}{2{x}^{2}+x-1}$$-\frac{3{x}^{3}}{x+1}$)÷(1-$\frac{x}{x+1}$)÷x2
=$\frac{4{x}^{3}-2{x}^{2}-6{x}^{4}+3{x}^{3}}{(2x-1)(x+1)}$÷$\frac{x+1-x}{x+1}$•$\frac{1}{{x}^{2}}$
=$\frac{-{x}^{2}(2x-1)(3x-2)}{(2x-1)(x+1)}$•(x+1)•$\frac{1}{{x}^{2}}$
=2-3x.
点评 本题主要考查分式的混合运算,通分、因式分解和约分是解答的关键.

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
(2)按照图中的方式继续排列餐桌,完成下表:
| 桌子张数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 可坐人数 |

(3)每增加-张桌子,可多坐4人;
(4)摆n张桌子时可坐4n+2人;
(5)一家餐厅有长方形桌子30张,现在有131个客人要吃饭,那该如何摆拼桌子?
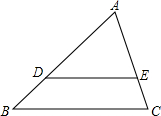 如图,在△ABC中,D,E分别是AB和AC上的点,且DE∥BC.
如图,在△ABC中,D,E分别是AB和AC上的点,且DE∥BC.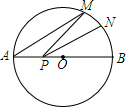 如图,AB是⊙O的直径,AB=10,点M在⊙O上,∠MAB=30°,N是弧MB的中点,P是直径AB上的一动点,若MN=2,则△PMN周长的最小值为5$\sqrt{2}$+2.
如图,AB是⊙O的直径,AB=10,点M在⊙O上,∠MAB=30°,N是弧MB的中点,P是直径AB上的一动点,若MN=2,则△PMN周长的最小值为5$\sqrt{2}$+2.