题目内容
18．
已知：如图，P是∠AOB的角平分线OC上的一点，⊙P与OA相交于E、F点，与OB相交于G、H点，则线段EF与GH的大小关系是EF=GH．
分析 作PM⊥AB于M，PN⊥GH于N，即作出弦EF、GH的弦心距，利用角平分线的性质可得PM=PN，然后利用同圆或等圆中，弦心距相等则对应的弦相等即可得EF=GH．
解答 
解：EF=GH．
理由：作PM⊥EF于M，PN⊥GH于N．
∵P是∠AOB的角平分线OC上的一点，
∴PM=PN，
∴EF=GH．
故答案为：EF=GH．
点评 本题考查的是垂径定理及角平分线的性质定理，以及弦与弦心距之间的关系定理，正确作出辅助线是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
如图所示，在菱形ABCD中，AB=4，∠BAD=120°，点E、F分别在菱形的边BC、CD上运动，且∠EAF=60°且E、F不与B、C、D重合，连接AC交EF于P点．
如图，在△ABC中，DE∥BC，$\frac{AD}{BD}$=$\frac{2}{3}$，则$\frac{DE}{BC}$=$\frac{2}{5}$．
如图，在△ABC中，∠C=90°，AD平分∠CAB，交BC于点D，CD=15cm，则点D到AB的距离是15cm．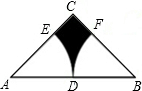
如图，Rt△ABC中，∠C=90°，AC=BC=4，点D是线段AB的中点，分别以点A，B为圆心，AD为半径画弧，分别交AC，BC于点E，F．则阴影部分面积为8-2π（结果保留π）．
7．下列各语句是真命题的是（ ）
| A． | 三个角对应相等的三角形全等 | |
| B． | 一组对边平行，另一组对边相等的四边形是平行四边形 | |
| C． | 三角形的内角和小于180° | |
| D． | 三角形的两边之和大于第三边 |
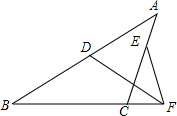如图，在△ABC中，F为BC延长线一点，D为AB上一点，且DB=DF，E为AC上一点，且EC=EF，∠A=40°，∠DFE的度数为（ ）