题目内容
8.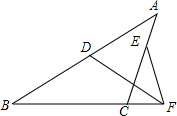 如图,在△ABC中,F为BC延长线一点,D为AB上一点,且DB=DF,E为AC上一点,且EC=EF,∠A=40°,∠DFE的度数为( )
如图,在△ABC中,F为BC延长线一点,D为AB上一点,且DB=DF,E为AC上一点,且EC=EF,∠A=40°,∠DFE的度数为( )| A. | 30 | B. | 35 | C. | 40 | D. | 50 |
分析 根据等腰三角形的性质得到∠B=∠DFB,∠ECF=∠EFC,根据三角形的外角的性质得到∠ECF=∠B+∠A,∠EFC=∠DFB+∠DFE,于是得到∠B+∠A=∠DFB+∠DFE,即可得到结论.
解答 解:∵DB=DF,
∴∠B=∠DFB,
∵EC=EF,
∴∠ECF=∠EFC,
∵∠ECF=∠B+∠A,∠EFC=∠DFB+∠DFE,
∴∠B+∠A=∠DFB+∠DFE,
∴∠DFE=∠A=40°,
故选C.
点评 本题考查了等腰三角形的性质,三角形是外角的性质,熟记等腰三角形的性质是解题的关键.

练习册系列答案
相关题目
19.若菱形的周长是40,则它的边长为( )
| A. | 20 | B. | 10 | C. | 15 | D. | 25 |
13.抛物线y=3x2+6x-12的对称轴是( )
| A. | x=-1 | B. | x=1 | C. | x=-2 | D. | x=2 |
 已知:如图,P是∠AOB的角平分线OC上的一点,⊙P与OA相交于E、F点,与OB相交于G、H点,则线段EF与GH的大小关系是EF=GH.
已知:如图,P是∠AOB的角平分线OC上的一点,⊙P与OA相交于E、F点,与OB相交于G、H点,则线段EF与GH的大小关系是EF=GH. 如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于P.
如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于P.