题目内容
6.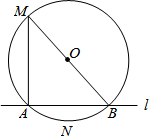 已知⊙O的半径是2,直线l与⊙O相交于A、B两点.M是⊙O上的一个动点,若∠AMB=45°,则△AMB面积的最大值是2$\sqrt{2}$+2.
已知⊙O的半径是2,直线l与⊙O相交于A、B两点.M是⊙O上的一个动点,若∠AMB=45°,则△AMB面积的最大值是2$\sqrt{2}$+2.
分析 过点O作OC⊥AB于C,交⊙O于D点,连结OA、OB、DA、DB根据圆周角定理推出△OAB为等腰直角三角形,求得AB=$\sqrt{2}$OA=2$\sqrt{2}$,当M点到AB的距离最大,△MAB的面积最大,即M点运动到D点,问题得解.
解答 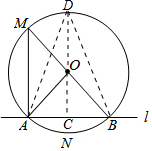 解:过点O作OC⊥AB于C,交⊙O于D点,连结OA、OB、DA、DB如图,
解:过点O作OC⊥AB于C,交⊙O于D点,连结OA、OB、DA、DB如图,
∵∠AMB=45°,
∴∠AOB=2∠AMB=90°,
∴△OAB为等腰直角三角形,
∴AB=$\sqrt{2}$OA=2$\sqrt{2}$,
∴当M点到AB的距离最大,△MAB的面积最大;即M点运动到D点,
∴△AMB面积的最大值=$\frac{1}{2}$×AB•DC=$\frac{1}{2}$×2$\sqrt{2}$×(2+$\sqrt{2}$)=2$\sqrt{2}$+2,
故答案为:2$\sqrt{2}$+2.
点评 本题考查了直线与圆的位置关系以及垂径定理和圆周角定理的运用,正确的作出辅助线是解题的关键.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
17.数3120000可以用科学记数法表示为( )
| A. | 3.12×106 | B. | 3.12×105 | C. | 0.312×106 | D. | 0.312×107 |
14.太阳核聚变反应释放的辐射能功率为3.8×1023千瓦,到达地球的仅占20亿分之一,到达地球的辐射能功率用科学记数法表示为( )千瓦.
| A. | 1.9×1014 | B. | 2.0×1014 | C. | 7.6×1015 | D. | 1.9×1015 |
11.10月24日成都第十五届西博会新疆代表团签约175亿元合作项目,175亿元用科学记数法表示为( )
| A. | 1.75×109元 | B. | 1.75×1010元 | C. | 0.175×1011元 | D. | 17.5×109元 |
18.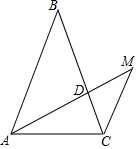 如图,若AB=BC,∠BAC=70°,AD=BD,CM∥AB交AD的延长线于点M,则∠M的大小是( )
如图,若AB=BC,∠BAC=70°,AD=BD,CM∥AB交AD的延长线于点M,则∠M的大小是( )
 如图,若AB=BC,∠BAC=70°,AD=BD,CM∥AB交AD的延长线于点M,则∠M的大小是( )
如图,若AB=BC,∠BAC=70°,AD=BD,CM∥AB交AD的延长线于点M,则∠M的大小是( )| A. | 60° | B. | 70° | C. | 30° | D. | 40° |
16.与算式23+23+23的运算结果相等的是( )
| A. | 23 | B. | 29 | C. | 3×23 | D. | 3×6 |
 已知直线l1:y=x+n-2与直线l2:y=mx+n相交于点P(1,2).
已知直线l1:y=x+n-2与直线l2:y=mx+n相交于点P(1,2).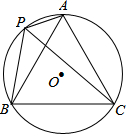 如图,⊙O的半径为1,A、P、B、C是⊙O上的四个点.∠APC=∠CPB=60°.则四边形APBC的最大面积是√3.
如图,⊙O的半径为1,A、P、B、C是⊙O上的四个点.∠APC=∠CPB=60°.则四边形APBC的最大面积是√3.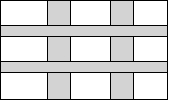 如图,在一块长为36米,宽为20米的矩形试验田中,计划挖两横、两竖四条水渠,横、竖水渠的宽度比为1:2,要使四条水渠所占面积是这块试验田面积的五分之一,求水渠的宽度.
如图,在一块长为36米,宽为20米的矩形试验田中,计划挖两横、两竖四条水渠,横、竖水渠的宽度比为1:2,要使四条水渠所占面积是这块试验田面积的五分之一,求水渠的宽度.