题目内容
11.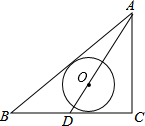 如图,△ABC中,∠C=90°,AC=3,AB=5,D为BC边的中点,以AD上一点O为圆心的⊙O和AB、BC均相切,则⊙O的半径为( )
如图,△ABC中,∠C=90°,AC=3,AB=5,D为BC边的中点,以AD上一点O为圆心的⊙O和AB、BC均相切,则⊙O的半径为( )| A. | 1 | B. | $\frac{6}{7}$ | C. | $\frac{2}{3}$ | D. | 1.5 |
分析 首先过点0作OE⊥AB于点E,OF⊥BC于点F.根据切线的性质,知OE、OF是⊙O的半径;然后由三角形的面积间的关系(S△ABO+S△BOD=S△ABD=S△ACD)列出关于圆的半径的等式,求得圆的半径即可.
解答 解:过点0作OE⊥AB于点E,OF⊥BC于点F.
∵AB、BC是⊙O的切线,
∴点E、F是切点,
∴OE、OF是⊙O的半径;
∴OE=OF;
在△ABC中,∠C=90°,AC=3,AB=5,
∴由勾股定理,得BC=4;
又∵D是BC边的中点,
∴S△ABD=S△ACD,
又∵S△ABD=S△ABO+S△BOD,
∴$\frac{1}{2}$AB•OE+$\frac{1}{2}$BD•OF=$\frac{1}{2}$CD•AC,
即5×OE+2×OE=2×3,
解得OE=$\frac{6}{7}$,
∴⊙O的半径是$\frac{6}{7}$.
故选B.
点评 本题考查了切线的性质与三角形的面积.注意运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
2.果农计划对果园加大种植密度,据测算,果园的总产量y(个)与增种果树的棵数x(棵)间的函数关系式为y=
-5x2+100x+60000,要使总产量在60320个以上,需要增加果树的棵数范围是( )
-5x2+100x+60000,要使总产量在60320个以上,需要增加果树的棵数范围是( )
| A. | 4≤x≤16 | B. | x≥6或x≤16 | C. | 4<x<16 | D. | x>6或x<16 |
6.近似数 3.65×105精确到的数位为( )
| A. | 百分位 | B. | 百位 | C. | 千位 | D. | 万位 |
16.与算式23+23+23的运算结果相等的是( )
| A. | 23 | B. | 29 | C. | 3×23 | D. | 3×6 |
3.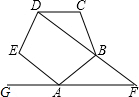 如图,正五边形ABCDE,AF∥CD,交DB的延长线于点F,则∠DFA=( )
如图,正五边形ABCDE,AF∥CD,交DB的延长线于点F,则∠DFA=( )
 如图,正五边形ABCDE,AF∥CD,交DB的延长线于点F,则∠DFA=( )
如图,正五边形ABCDE,AF∥CD,交DB的延长线于点F,则∠DFA=( )| A. | 108° | B. | 72° | C. | 36° | D. | 30° |
1.用火柴棍象如图这样搭三角形:你能找出规律猜想出下列问题吗?搭n个三角形需要( )根火柴棍.


| A. | 2n | B. | 2n+1 | C. | 2n-1 | D. | 3n. |
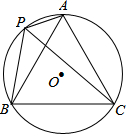 如图,⊙O的半径为1,A、P、B、C是⊙O上的四个点.∠APC=∠CPB=60°.则四边形APBC的最大面积是√3.
如图,⊙O的半径为1,A、P、B、C是⊙O上的四个点.∠APC=∠CPB=60°.则四边形APBC的最大面积是√3. 如图,直线AB、CD相交于点O,OE平分∠AOD,∠DOE=30°,求∠BOC的度数.
如图,直线AB、CD相交于点O,OE平分∠AOD,∠DOE=30°,求∠BOC的度数.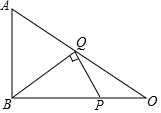 如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=8,P是BC边上一动点,设BP=x,若能在AC边上找一点Q,使∠BQP=90°,则x的范围是6≤x≤8.
如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=8,P是BC边上一动点,设BP=x,若能在AC边上找一点Q,使∠BQP=90°,则x的范围是6≤x≤8.