题目内容
12.根据图形填空:
①n=30
②x=40
③y=55
④n=45.
分析 根据三角形的内角和和三角形的外角的性质即可得到结论.
解答 解:n=180-80-70=30,
x=$\frac{1}{2}$(180-100)=40,
y=90-35=55,
n=110-65=45.
故答案为:30.40.55.45.
点评 本题考查了三角形的内角和和三角形的外角的性质,熟记三角形的内角和是解题的关键.

练习册系列答案
相关题目
18.在实数0,(-$\sqrt{3}$)0,(-$\frac{2}{3}$)-2,|-2|中,最大的是( )
| A. | 0 | B. | (-$\sqrt{3}$)0 | C. | (-$\frac{2}{3}$)-2 | D. | |-2| |
17.数3120000可以用科学记数法表示为( )
| A. | 3.12×106 | B. | 3.12×105 | C. | 0.312×106 | D. | 0.312×107 |
4.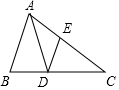 如图,已知AD为△ABC的角平分线,DE∥AB交AC于E,如果$\frac{AE}{EC}$=$\frac{3}{5}$,那么$\frac{AC}{AB}$等于( )
如图,已知AD为△ABC的角平分线,DE∥AB交AC于E,如果$\frac{AE}{EC}$=$\frac{3}{5}$,那么$\frac{AC}{AB}$等于( )
 如图,已知AD为△ABC的角平分线,DE∥AB交AC于E,如果$\frac{AE}{EC}$=$\frac{3}{5}$,那么$\frac{AC}{AB}$等于( )
如图,已知AD为△ABC的角平分线,DE∥AB交AC于E,如果$\frac{AE}{EC}$=$\frac{3}{5}$,那么$\frac{AC}{AB}$等于( )| A. | $\frac{3}{5}$ | B. | $\frac{5}{3}$ | C. | $\frac{8}{5}$ | D. | $\frac{3}{2}$ |
2.果农计划对果园加大种植密度,据测算,果园的总产量y(个)与增种果树的棵数x(棵)间的函数关系式为y=
-5x2+100x+60000,要使总产量在60320个以上,需要增加果树的棵数范围是( )
-5x2+100x+60000,要使总产量在60320个以上,需要增加果树的棵数范围是( )
| A. | 4≤x≤16 | B. | x≥6或x≤16 | C. | 4<x<16 | D. | x>6或x<16 |
 如图,△ABC中,DE∥BC,则$\frac{AB}{()}$=$\frac{()}{()}$.
如图,△ABC中,DE∥BC,则$\frac{AB}{()}$=$\frac{()}{()}$.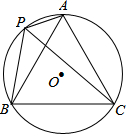 如图,⊙O的半径为1,A、P、B、C是⊙O上的四个点.∠APC=∠CPB=60°.则四边形APBC的最大面积是√3.
如图,⊙O的半径为1,A、P、B、C是⊙O上的四个点.∠APC=∠CPB=60°.则四边形APBC的最大面积是√3.