题目内容
5.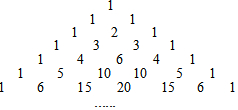 杨辉是我国南宋时期杰出的数学家和教育家,如图是杨辉在公元1261年著作《详解九章算法》里面的一张图,即“杨辉三角”,该图中有很多规律,请仔细观察,解答下列问题:
杨辉是我国南宋时期杰出的数学家和教育家,如图是杨辉在公元1261年著作《详解九章算法》里面的一张图,即“杨辉三角”,该图中有很多规律,请仔细观察,解答下列问题:(1)图中给出了七行数字,根据构成规律,第8行中从左边数第3个数是21;
(2)利用不完全归纳法探索出第n行中的所有数字之和为2n-1.
分析 (1)设第n行第2个数为an(n≥2,n为正整数),第n行第3个数为bn(n≥3,n为正整数),根据给定“杨辉三角”的部分找出an、bn的值,根据数的变化找出变化规律“an=n-1,bn=$\frac{(n-1)(n-2)}{2}$”,依此规律即可得出结论;
(2)由题意得出每行的数字之和等于2的序数减一次幂,据此解答即可.
解答 解:(1)设第n行第2个数为an(n≥2,n为正整数),第n行第3个数为bn(n≥3,n为正整数),
观察,发现规律:
∵a2=1,a3=2,a4=3,a5=4,a6=5,
∴an=n-1;
∵b3=1,b4=3=1+2=b3+2,b5=6=3+3=b4+3,b6=10=6+4=b5+4,…,
∴bn-bn-1=n-2,
∴bn=b3+b4-b3+b5-b4+b6-b5+…+bn-bn-1=1+2+3+…+n-2=$\frac{(n-1)(n-2)}{2}$.
当n=8时,b3=$\frac{(8-1)(8-2)}{2}$=21;
(2)∵第1行数字之和1=20,
第2行数字之和2=21,
第3行数字之和4=22,
第4行数字之和8=23,
…
∴第n行数字之和为2n-1.
故答案为:21;2n-1.
点评 本题主要考查数字的变化类,解题的关键是每行的数相加,分析总结得出规律,根据规律求出第n行的数据之和.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
4.已知正比例函数y=ax(a≠0)与反比例函数y=$\frac{k}{x}$(k≠0)图象的一个交点坐标为(-1,-1),则另一个交点坐标是( )
| A. | (1,-1) | B. | (1,1) | C. | (-1,1) | D. | (0,1) |
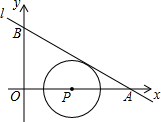 我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”.如图,直线l:y=kx+3$\sqrt{3}$与轴、轴分别交于A、B,∠OAB=30°,点P在轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是4.
我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”.如图,直线l:y=kx+3$\sqrt{3}$与轴、轴分别交于A、B,∠OAB=30°,点P在轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是4.