题目内容
7.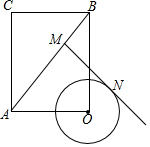 如图,在矩形AOBC中,AO=3,BO=4,⊙O的半径为1,点M是矩形对角线AB边上的动点,过点M做⊙O的一条切线MN,切点为N,则切线长MN的最小值是$\frac{\sqrt{119}}{5}$.
如图,在矩形AOBC中,AO=3,BO=4,⊙O的半径为1,点M是矩形对角线AB边上的动点,过点M做⊙O的一条切线MN,切点为N,则切线长MN的最小值是$\frac{\sqrt{119}}{5}$.
分析 由MN为⊙O切线,推出ON⊥MN,在Rt△OMN中,MN=$\sqrt{O{M}^{2}-O{N}^{2}}$=$\sqrt{O{M}^{2}-{1}^{2}}$,当OM最小时,MN最小,而当OM⊥AB时,OM最小,此时OM=$\frac{OA•OB}{AB}$,由此即可解决问题.
解答 解:连结ON、如图,
在Rt△AOB中,∵OA=3,OB=4,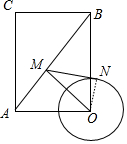
∴AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵MN为⊙O切线,
∴ON⊥MN,
在Rt△OMN中,MN=$\sqrt{O{M}^{2}-O{N}^{2}}$=$\sqrt{O{M}^{2}-{1}^{2}}$,
当OM最小时,MN最小,
而当OM⊥AB时,OM最小,此时OM=$\frac{OA•OB}{AB}$=$\frac{12}{5}$,
∴MN的最小值为=$\sqrt{(\frac{12}{5})^{2}-1}$=$\frac{\sqrt{119}}{5}$.
故答案为$\frac{\sqrt{119}}{5}$.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
相关题目
17.小明与爸爸的年龄和是52岁,爸爸对小明说:“当我的年龄是你现在的年龄的时候,你还要16年才出生呢.”如果设现在小明的年龄是x岁,爸爸的年龄是y岁,那么下面方程组正确的是( )
| A. | $\left\{\begin{array}{l}{x+52=y}\\{x+16=y-x}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{y-x=52}\\{x-16=y-x}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+y=52}\\{y-2x=16}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{y=52-x}\\{x-16=y-x}\end{array}\right.$ |
 如图所示,以Rt△ABC的直角边BC为直径向外作半圆,则该半圆的面积为18π.
如图所示,以Rt△ABC的直角边BC为直径向外作半圆,则该半圆的面积为18π.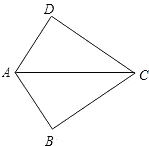 如图所示,∠D=∠B=90°,请你添加一个适当的条件AB=AD,使△ABC≌△ADC.(只需添加一个即可)
如图所示,∠D=∠B=90°,请你添加一个适当的条件AB=AD,使△ABC≌△ADC.(只需添加一个即可)