题目内容
15.在△ABC中,AB=6,AC=8,在△A′B′C′中,A′B′=4,A′C′=3,若BC:B′C′=2:1,则△ABC∽△A′C′B′.分析 通过计算得出$\frac{AB}{A′C′}=\frac{AC}{A′B′}$=2,得出当BC:B′C′=2:1时,△ABC∽△A′C′B′即可.
解答 解:∵$\frac{AB}{A′C′}=\frac{6}{3}$=2,$\frac{AC}{A′B′}=\frac{8}{4}$=2,
∴$\frac{AB}{A′C′}=\frac{AC}{A′B′}$=2,
∴当BC:B′C′=2:1时,
则△ABC∽△A′C′B′.
故答案为:2:1;△A′C′B′.
点评 本题考查了相似三角形的判定方法;熟练掌握相似三角形的判定方法,通过计算得出两边成比例是解决问题的关键.

练习册系列答案
相关题目
 如图所示,长方形内有两个相邻的正方形,面积分别为9和a2(a>0),那么阴影部分的面积为3a-a2.
如图所示,长方形内有两个相邻的正方形,面积分别为9和a2(a>0),那么阴影部分的面积为3a-a2. 已知a、b、c在数轴上的位置如图.
已知a、b、c在数轴上的位置如图.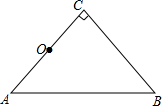 如图所示,在等腰直角三角形ABC中,∠C=90°,AC=2cm,如果以AC的中点O为旋转中心,将△ABC逆时针旋转90°;
如图所示,在等腰直角三角形ABC中,∠C=90°,AC=2cm,如果以AC的中点O为旋转中心,将△ABC逆时针旋转90°;