题目内容
5.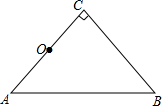 如图所示,在等腰直角三角形ABC中,∠C=90°,AC=2cm,如果以AC的中点O为旋转中心,将△ABC逆时针旋转90°;
如图所示,在等腰直角三角形ABC中,∠C=90°,AC=2cm,如果以AC的中点O为旋转中心,将△ABC逆时针旋转90°;(1)画出△ABC旋转后的△A′B′C′;
(2)求BB′的长.
分析 (1)过点O作OA′⊥AC交AB于A′,反向延长OA′到C′使OC′=OC,然后作B′C′⊥OC′且使B′C′=AC,这样可得到△A′B′C′;
(2)先利用勾股定理计算出OB=$\sqrt{5}$,再根据旋转的性质得OB=OB′=$\sqrt{5}$,∠BOB′=90°,则△OBB′为等腰直角三角形,所以BB′=$\sqrt{2}$OB=$\sqrt{10}$.
解答 解:(1)如图,△A′B′C′为所作;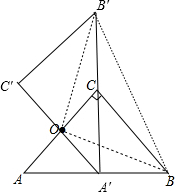
(2)∵△ABC为等腰直角三角形,
∴BC=AC=2,
而OC=$\frac{1}{2}$AC=1,
∴OB=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
∵△AB绕点O逆时针旋转90°得到△A′B′C′,
∴OB=OB′=$\sqrt{5}$,∠BOB′=90°,
∴△OBB′为等腰直角三角形,
∴BB′=$\sqrt{2}$OB=$\sqrt{10}$.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
13.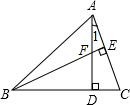 如图,AD,BE为△ABC的两条高,∠1=30°,则下列结论不正确的是( )
如图,AD,BE为△ABC的两条高,∠1=30°,则下列结论不正确的是( )
 如图,AD,BE为△ABC的两条高,∠1=30°,则下列结论不正确的是( )
如图,AD,BE为△ABC的两条高,∠1=30°,则下列结论不正确的是( )| A. | AC=2CD | B. | BC=2CE | C. | CD=CE | D. | AF=2EF |
14.下列因式分解错误的是 ( )
| A. | -$\frac{1}{2}$+8x2=-$\frac{1}{2}$(1-4x)(1+4x) | B. | 16x2-4=(4x+2)(4x-2) | ||
| C. | m2+m+$\frac{1}{4}$=(m+$\frac{1}{2}$)2 | D. | -x2+4y2=(x+2y)(2y-x) |
 如图,等边三角形ABC内接于⊙O,D是AB上的一点,则∠ADB=120°.
如图,等边三角形ABC内接于⊙O,D是AB上的一点,则∠ADB=120°. 如图,已知抛物线y=ax2+bx+3经过点B(3,0),C(4,3),与y轴交于点A,把抛物线向上平移,使得顶点E落在x轴上点F处,点A平移至点D处,则两条抛物线、对称轴EF和y轴围成的图形(图中阴影部分)的面积S=2.
如图,已知抛物线y=ax2+bx+3经过点B(3,0),C(4,3),与y轴交于点A,把抛物线向上平移,使得顶点E落在x轴上点F处,点A平移至点D处,则两条抛物线、对称轴EF和y轴围成的图形(图中阴影部分)的面积S=2.