题目内容
4. 已知a、b、c在数轴上的位置如图.
已知a、b、c在数轴上的位置如图.(1)试比较a,-a,b,-b,c,-c的大小;
(2)化简:|a-b|+|b+c|+|b-c|.
分析 (1)根据a、b、c在数轴上的位置,可得c<a<0<b,-c>b>-a,据此判断出a,-a,b,-b,c,-c的大小关系即可.
(2)首先判断出a-b、b+c、b-c的正负,然后求出|a-b|+|b+c|+|b-c|的值是多少即可.
解答 解:(1)根据a、b、c在数轴上的位置,可得
c<a<0<b,-c>b>-a,
∴c<-b<a<-a<b<-c.
(2)∵c<a<0<b,-c>b>-a,
∴a-b<0,b+c<0,b-c>0,
∴|a-b|+|b+c|+|b-c|
=b-a-(b+c)+b-c
=-a+b-2c
点评 (1)此题主要考查了有理数大小比较的方法,要熟练掌握,解答此题的关键是要明确:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小.
(2)此题还考查了数轴的特征和应用,要熟练掌握,解答此题的关键是要明确:一般来说,当数轴方向朝右时,右边的数总比左边的数大.
(3)此题还考查了绝对值的求法,以及整式的加减运算,要熟练掌握.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
13.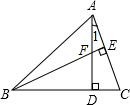 如图,AD,BE为△ABC的两条高,∠1=30°,则下列结论不正确的是( )
如图,AD,BE为△ABC的两条高,∠1=30°,则下列结论不正确的是( )
 如图,AD,BE为△ABC的两条高,∠1=30°,则下列结论不正确的是( )
如图,AD,BE为△ABC的两条高,∠1=30°,则下列结论不正确的是( )| A. | AC=2CD | B. | BC=2CE | C. | CD=CE | D. | AF=2EF |
14.下列因式分解错误的是 ( )
| A. | -$\frac{1}{2}$+8x2=-$\frac{1}{2}$(1-4x)(1+4x) | B. | 16x2-4=(4x+2)(4x-2) | ||
| C. | m2+m+$\frac{1}{4}$=(m+$\frac{1}{2}$)2 | D. | -x2+4y2=(x+2y)(2y-x) |

 如图,D,E,F,B四点共线,AB∥CD,∠AEB=∠CFD,BF=DE.求证.AE=CF.
如图,D,E,F,B四点共线,AB∥CD,∠AEB=∠CFD,BF=DE.求证.AE=CF.