题目内容
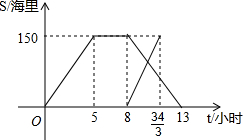 一天,某渔船离开港口前往黄岩岛海域捕鱼,8小时后返航,此时一艘渔政船从该港口出发前往黄岩岛巡查(假设渔政船与渔船沿同一航线航行).下图是渔政船及渔船到港口的距离S和渔船离开港口的时间t之间的函数图象.
一天,某渔船离开港口前往黄岩岛海域捕鱼,8小时后返航,此时一艘渔政船从该港口出发前往黄岩岛巡查(假设渔政船与渔船沿同一航线航行).下图是渔政船及渔船到港口的距离S和渔船离开港口的时间t之间的函数图象.(1)写出渔船离港口的距离S和它离开港口的时间t的函数关系式;
(2)在渔船返航途中,什么时间范围内两船间距离不超过30海里?
考点:一次函数的应用
专题:
分析:(1)根据函数图象可以得出是一个分段函数,当0≤t≤5时,5<t≤8时,8<t≤13时,由待定系数法就可以求出结论;
(2)由待定系数法求出渔政船离港口的距离S和它离开港口的时间t的函数关系式,再建立不等式组求出其解即可.
(2)由待定系数法求出渔政船离港口的距离S和它离开港口的时间t的函数关系式,再建立不等式组求出其解即可.
解答:解:(1)当0≤t≤5时,设渔船离港口的距离S和它离开港口的时间t的关系式为S=k1t,由题意,得
150=5k1,
解得:k1=30
∴S=30t;
5<t≤8时,S=150
当8<t≤13时,设渔船离港口的距离S和它离开港口的时间t的关系式为S=k2t+b,由题意,得
,
解得:
,
∴S=-30t+390.
∴S=
;
(2)渔政船离港口的距离S和它离开港口的时间t的函数关系式为S1=k3t+b1,由题意,得
,
解得:
,
∴S1=45t-360,
∴
,
∴9.6≤t≤10.4,
∴9.6≤t≤10.4时,两船距离不超过30海里.
150=5k1,
解得:k1=30
∴S=30t;
5<t≤8时,S=150
当8<t≤13时,设渔船离港口的距离S和它离开港口的时间t的关系式为S=k2t+b,由题意,得
|
解得:
|
∴S=-30t+390.
∴S=
|
(2)渔政船离港口的距离S和它离开港口的时间t的函数关系式为S1=k3t+b1,由题意,得
|
解得:
|
∴S1=45t-360,
∴
|
∴9.6≤t≤10.4,
∴9.6≤t≤10.4时,两船距离不超过30海里.
点评:本题考查了分段函数的在实际问题中的运用,待定系数法求一次函数的解析式的运用,列不等式组解实际问题的运用,解答时求出一次函数的解析式是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
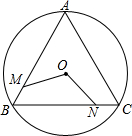 如图,M、N分别是⊙O的内接正△ABC的边AB、BC上的点且BM=CN,连接OM、ON,求∠MON的度数.
如图,M、N分别是⊙O的内接正△ABC的边AB、BC上的点且BM=CN,连接OM、ON,求∠MON的度数.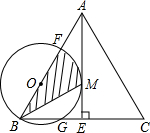 如图△ABC中,AB=AC,AE⊥BC,E为垂足,F为AB上一点.以BF为直径的圆与AE相切于M点,交BC于G点.
如图△ABC中,AB=AC,AE⊥BC,E为垂足,F为AB上一点.以BF为直径的圆与AE相切于M点,交BC于G点. 关于x的一元二次方程x2+(m+2)x+
关于x的一元二次方程x2+(m+2)x+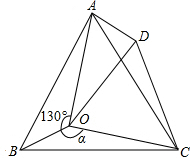 如图,点O是等边三角形ABC内的一点,∠AOB=130°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得到△ADC,连接OD.
如图,点O是等边三角形ABC内的一点,∠AOB=130°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得到△ADC,连接OD.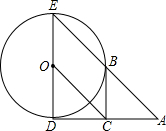 如图,已知⊙O的半径为1,DE是⊙O的直径,过D点作⊙O的切线AD,C是AD的中点,AE交⊙O于B点,若四边形BCOE是平行四边形,
如图,已知⊙O的半径为1,DE是⊙O的直径,过D点作⊙O的切线AD,C是AD的中点,AE交⊙O于B点,若四边形BCOE是平行四边形, 如图,已知点A为反比例函数y=
如图,已知点A为反比例函数y=