题目内容
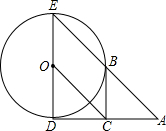 如图,已知⊙O的半径为1,DE是⊙O的直径,过D点作⊙O的切线AD,C是AD的中点,AE交⊙O于B点,若四边形BCOE是平行四边形,
如图,已知⊙O的半径为1,DE是⊙O的直径,过D点作⊙O的切线AD,C是AD的中点,AE交⊙O于B点,若四边形BCOE是平行四边形,(1)求AD的长;
(2)求证:BC是⊙O的切线.
考点:切线的判定与性质,平行四边形的性质
专题:
分析:(1)连接OB,根据四边形BCOE为平行四边形,可得BC∥OE,BC=OE,即BC∥OD,BC=OE=OD,从而得出四边形BCDO为平行四边形,又因为OB=OD,AD为切线,则∠ODC=90°,即四边形BCDO为正方形,所以AD=2CD=2;
(2)由四边形BCDO为正方形,则∠OBC=90°,从而得出BC为圆O的切线.
(2)由四边形BCDO为正方形,则∠OBC=90°,从而得出BC为圆O的切线.
解答: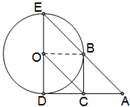 证明:(1)连接OB
证明:(1)连接OB
∵四边形BCOE为平行四边形.
∴BC∥OE,BC=OE,
即BC∥OD,BC=OE=OD,
∴四边形BCDO为平行四边形,
又OB=OD,AD为切线,∴∠ODC=90°,
∴四边形BCDO为正方形,
故AD=2CD=2.
(2)证明:∵四边形BCDO为正方形(已证).
∴∠OBC=90°.
∴BC为圆O的切线.
 证明:(1)连接OB
证明:(1)连接OB∵四边形BCOE为平行四边形.
∴BC∥OE,BC=OE,
即BC∥OD,BC=OE=OD,
∴四边形BCDO为平行四边形,
又OB=OD,AD为切线,∴∠ODC=90°,
∴四边形BCDO为正方形,
故AD=2CD=2.
(2)证明:∵四边形BCDO为正方形(已证).
∴∠OBC=90°.
∴BC为圆O的切线.
点评:本题考查了切线的判定和性质以及平行四边形现在的综合运用,要熟练掌握.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
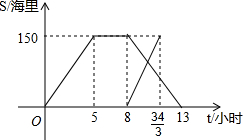 一天,某渔船离开港口前往黄岩岛海域捕鱼,8小时后返航,此时一艘渔政船从该港口出发前往黄岩岛巡查(假设渔政船与渔船沿同一航线航行).下图是渔政船及渔船到港口的距离S和渔船离开港口的时间t之间的函数图象.
一天,某渔船离开港口前往黄岩岛海域捕鱼,8小时后返航,此时一艘渔政船从该港口出发前往黄岩岛巡查(假设渔政船与渔船沿同一航线航行).下图是渔政船及渔船到港口的距离S和渔船离开港口的时间t之间的函数图象.