题目内容
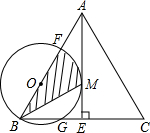 如图△ABC中,AB=AC,AE⊥BC,E为垂足,F为AB上一点.以BF为直径的圆与AE相切于M点,交BC于G点.
如图△ABC中,AB=AC,AE⊥BC,E为垂足,F为AB上一点.以BF为直径的圆与AE相切于M点,交BC于G点.(1)求证:BM平分∠ABC;
(2)当BC=4,cosC=
| 1 |
| 2 |
①求⊙O的半径;
②求图中阴影部分的面积.(结果保留π与根号)
考点:切线的性质,扇形面积的计算
专题:计算题
分析:(1)连OM,根据切线的性质得OM⊥AE,而AE⊥BC,则OM∥BC,根据平行线的性质得∠OMB=∠MBC,而∠OBM=∠OMB,所以∠OBM=∠MBE;
(2)①设⊙O的半径为R,根据等腰三角形的性质得BE=CE=2,由cos∠C=
得到∠C=60°,则可判断△ABC为等边三角形,所以AB=AC=BC=4,则∠OAM=30°,根据含30度的直角三角形三边的关系得到AO=2R,则2R+R=4,解得R=
;
②过O作OH⊥BM,H为垂足,根据垂径定理得BH=MH,易得∠AOM=60°,∠ABH=30°,根据含30度的直角三角形三边的关系可得OH=
OB=
,BH=
OH=
,所以BM=
,然后根据扇形面积公式和三角形面积公式和S阴=S扇形FOM+S△OBM进行计算.
(2)①设⊙O的半径为R,根据等腰三角形的性质得BE=CE=2,由cos∠C=
| 1 |
| 2 |
| 4 |
| 3 |
②过O作OH⊥BM,H为垂足,根据垂径定理得BH=MH,易得∠AOM=60°,∠ABH=30°,根据含30度的直角三角形三边的关系可得OH=
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 3 |
| 4 |
| 3 |
| 3 |
解答:(1)证明:连OM,如图,
∵⊙O与AE相切于M,
∴OM⊥AE,
∵AE⊥BC,
∴OM∥BC,
∴∠OMB=∠MBC,
∵OB=OM,
∴∠OBM=∠OMB,
∴∠OBM=∠MBE,
∴BM平分∠ABC;
(2)解:①设⊙O的半径为R,
∵AB=AC,BC=4,AE⊥BC,
∴BE=CE=2,
在Rt△ACE中,cos∠C=
,
∴∠C=60°
∴△ABC为等边三角形,
∴AB=AC=BC=4,
∴∠OAM=30°,
∴AO=2R,
而AB=OA+BO,
∴2R+R=4,
∴R=
,
即⊙O的半径为
;
②过O作OH⊥BM,H为垂足,如图,
∵OH⊥BM,
∴BH=MH,
∵OM∥BE,
∴∠AOM=60°,
∴∠ABH=30°,
∴OH=
OB=
,BH=
OH=
,
∴BM=
,
∴S△OBM=
OH•BM=
,
而S扇形FOM=
=
π,
∴S阴=S扇形FOM+S△OBM=
π+
.
∵⊙O与AE相切于M,

∴OM⊥AE,
∵AE⊥BC,
∴OM∥BC,
∴∠OMB=∠MBC,
∵OB=OM,
∴∠OBM=∠OMB,
∴∠OBM=∠MBE,
∴BM平分∠ABC;
(2)解:①设⊙O的半径为R,
∵AB=AC,BC=4,AE⊥BC,
∴BE=CE=2,
在Rt△ACE中,cos∠C=
| 1 |
| 2 |
∴∠C=60°
∴△ABC为等边三角形,
∴AB=AC=BC=4,
∴∠OAM=30°,
∴AO=2R,
而AB=OA+BO,
∴2R+R=4,
∴R=
| 4 |
| 3 |
即⊙O的半径为
| 4 |
| 3 |
②过O作OH⊥BM,H为垂足,如图,
∵OH⊥BM,
∴BH=MH,
∵OM∥BE,
∴∠AOM=60°,
∴∠ABH=30°,
∴OH=
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 3 |
∴BM=
| 4 |
| 3 |
| 3 |
∴S△OBM=
| 1 |
| 2 |
| 4 |
| 9 |
| 3 |
而S扇形FOM=
60π×
| ||
| 360 |
| 8 |
| 27 |
∴S阴=S扇形FOM+S△OBM=
| 8 |
| 27 |
| 4 |
| 9 |
| 3 |
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了扇形的面积公式和含30度的直角三角形三边的关系.

练习册系列答案
相关题目
 如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连结CE.
如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连结CE.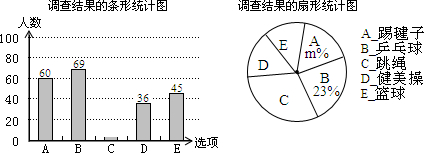
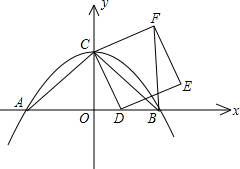 已知抛物线y=-
已知抛物线y=-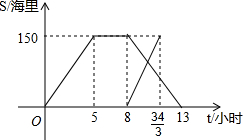 一天,某渔船离开港口前往黄岩岛海域捕鱼,8小时后返航,此时一艘渔政船从该港口出发前往黄岩岛巡查(假设渔政船与渔船沿同一航线航行).下图是渔政船及渔船到港口的距离S和渔船离开港口的时间t之间的函数图象.
一天,某渔船离开港口前往黄岩岛海域捕鱼,8小时后返航,此时一艘渔政船从该港口出发前往黄岩岛巡查(假设渔政船与渔船沿同一航线航行).下图是渔政船及渔船到港口的距离S和渔船离开港口的时间t之间的函数图象.