题目内容
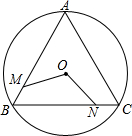如图，M、N分别是⊙O的内接正△ABC的边AB、BC上的点且BM=CN，连接OM、ON，求∠MON的度数．考点：三角形的外接圆与外心,全等三角形的判定与性质,等边三角形的性质
专题：
分析：证明△OBM≌△OCN就可以证明∠MOB=∠NOC，从而得到∠MON=∠BOC即可求解．
解答：
解：连接OB、OC；
∵△ABC是⊙O的内接正三角形，
∴OB=OC，∠BOC=120°，∠OBC=∠OCB=∠OBA=30°；
在△OBM和△OCN中，
，
∴△OBM≌△OCN（SAS），
∴∠MOB=∠NOC，
∴∠MON=∠BOC=120°．
解：连接OB、OC；∵△ABC是⊙O的内接正三角形，
∴OB=OC，∠BOC=120°，∠OBC=∠OCB=∠OBA=30°；
在△OBM和△OCN中，
|
∴△OBM≌△OCN（SAS），
∴∠MOB=∠NOC，
∴∠MON=∠BOC=120°．
点评：此题主要考查了全等三角形的判定与性质以及等边三角形的性质，得出△OBM≌△OCN是解题关键．
练习册系列答案
阅读快车系列答案
相关题目
下列运算正确的是（ ）
| A、3a+2a=5a2 | ||
B、
| ||
| C、x2+x2=2x2 | ||
| D、x6÷x2=x3 |
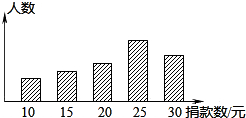为支持我国西南地区抗旱救灾，团中央和全国少工委号召全国各级共青团和少先队组织，积极组织动员广大共青团员和少先队员，每人捐助一瓶水，用实际行动向灾区人民群众送去“爱心水”． 某校对本校倡导的自愿捐款活动进行抽样调查，得到了一组学生捐款情况的数据．如图是根据这组数据绘制的统计图，图中从左到右各长方形的高度之比为3：4：5：8：6，又知此次调查中捐款25元和30元的学生一共42人．请你根据上述信息解答下列问题：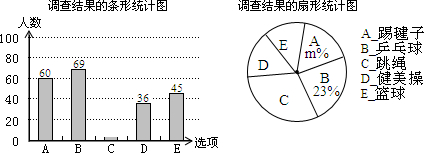
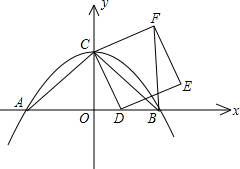已知抛物线y=-
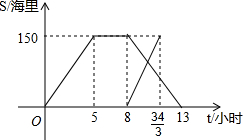一天，某渔船离开港口前往黄岩岛海域捕鱼，8小时后返航，此时一艘渔政船从该港口出发前往黄岩岛巡查（假设渔政船与渔船沿同一航线航行）．下图是渔政船及渔船到港口的距离S和渔船离开港口的时间t之间的函数图象．