题目内容
6.△ABC中,∠ACB=90°,CD⊥AB于点D,∠A=30°,BD=1.5cm,则AD=4.5cm.分析 根据同角的余角相等求出∠BCD=∠A=30°,再根据30°角所对的直角边等于斜边的一半求出BC、AB的长,然后根据AD=AB-BD计算即可得解.
解答  解:∵∠ACB=90°,CD⊥AB,
解:∵∠ACB=90°,CD⊥AB,
∴∠BCD+∠ACD=90°,∠A+∠ACD=90°,
∴∠BCD=∠A=30°,
∵BD=1.5cm,
∴BC=2BD=3cm,AB=2BC=6cm,
∴AD=AB-BD=4.5cm.
故答案是:4.5.
点评 本题主要考查了直角三角形30°角所对的直角边等于斜边的一半的性质,同角的余角相等的性质,熟记性质是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11. 如图,直线AB和CD相交于点O,OE⊥AB,∠AOC=30°,则∠DOE的度数是( )
如图,直线AB和CD相交于点O,OE⊥AB,∠AOC=30°,则∠DOE的度数是( )
 如图,直线AB和CD相交于点O,OE⊥AB,∠AOC=30°,则∠DOE的度数是( )
如图,直线AB和CD相交于点O,OE⊥AB,∠AOC=30°,则∠DOE的度数是( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
 如图,在平面直角坐标系中,顶点为M的抛物线y=ax2+bx(a>0)经过点A和x轴正半轴上的点B,AO=BO=2,∠AOB=120°.
如图,在平面直角坐标系中,顶点为M的抛物线y=ax2+bx(a>0)经过点A和x轴正半轴上的点B,AO=BO=2,∠AOB=120°.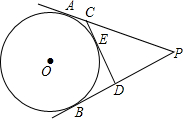 如图,PA、PB切⊙O于点A、B,PA=6,CD切⊙O于点E,交PA、PB于C、D两点,则△PCD的周长是12.
如图,PA、PB切⊙O于点A、B,PA=6,CD切⊙O于点E,交PA、PB于C、D两点,则△PCD的周长是12. 如图,在一张面积为48cm2的正方形硬纸板的四周各剪去一个同样大小的面积为3cm2的小正方形,再折合成一个无盖的长方体盒子(纸板的厚度忽略不计),那么这个长方体盒子的体积是多少?
如图,在一张面积为48cm2的正方形硬纸板的四周各剪去一个同样大小的面积为3cm2的小正方形,再折合成一个无盖的长方体盒子(纸板的厚度忽略不计),那么这个长方体盒子的体积是多少?