题目内容
15.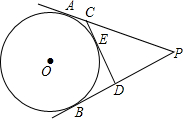 如图,PA、PB切⊙O于点A、B,PA=6,CD切⊙O于点E,交PA、PB于C、D两点,则△PCD的周长是12.
如图,PA、PB切⊙O于点A、B,PA=6,CD切⊙O于点E,交PA、PB于C、D两点,则△PCD的周长是12.
分析 由PA,PB切⊙O于A、B两点,CD切⊙O于点E,根据切线长定理可得:PB=PA=6,CA=CE,DB=DE,继而可得△PCD的周长=PA+PB.
解答 解:∵PA,PB切⊙O于A、B两点,CD切⊙O于点E,
∴PB=PA=6,CA=CE,DB=DE,
∴△PCD的周长=PC+CE+PD=PC+CE+DE+PC=PC+CA+DB+PD=PA+PB=12.
故答案为:12.
点评 此题考查了切线长定理.此题难度不大,注意从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线,平分两条切线的夹角.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.下面给出的四个语句,其中正确的有( )
①等角的余角相等;
②一个角的补角一定大于这个角;
③有理数分为正数和负数;
④零是最小的正数;
⑤过直线外一点可以作一条以上的直线与已知直线平行.
①等角的余角相等;
②一个角的补角一定大于这个角;
③有理数分为正数和负数;
④零是最小的正数;
⑤过直线外一点可以作一条以上的直线与已知直线平行.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
7.下列命题中,是真命题的是( )
| A. | 三个点确定一个圆 | |
| B. | 同弧所对的圆周角与圆心角相等 | |
| C. | 直径是圆中最长的弦 | |
| D. | 圆是轴对称图形,不是中心对称图形 |
5.若(a+$\sqrt{2}$)2与|b-1|互为相反数,则2b-a的值为( )
| A. | 2$\sqrt{2}$ | B. | $\sqrt{2}$+2 | C. | $\sqrt{2}$-2 | D. | 2-$\sqrt{2}$ |
 在一条笔直的公路L的两侧,分别有A.B两个村庄,如图,现在要在公路上建一个汽车站P,使汽车站P到两村的距离和最小,请在图中画出汽车站P的位置,请说明理由.
在一条笔直的公路L的两侧,分别有A.B两个村庄,如图,现在要在公路上建一个汽车站P,使汽车站P到两村的距离和最小,请在图中画出汽车站P的位置,请说明理由.
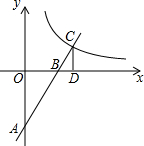 如图,直线y=2x-4的图象与x、y轴交于B、A两点,与y=$\frac{k}{x}$的图象交于点C,CD⊥x轴于点D,如果△CDB的面积:△AOB的面积=1:4,则k的值为6.
如图,直线y=2x-4的图象与x、y轴交于B、A两点,与y=$\frac{k}{x}$的图象交于点C,CD⊥x轴于点D,如果△CDB的面积:△AOB的面积=1:4,则k的值为6.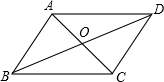 如图,在平行四边形ABCD中,连接AC,BD并相交于点O,你发现0A与OC,OB与0D有什么数量关系?并证明你发现的结论.
如图,在平行四边形ABCD中,连接AC,BD并相交于点O,你发现0A与OC,OB与0D有什么数量关系?并证明你发现的结论.