题目内容
18. 如图,在平面直角坐标系中,顶点为M的抛物线y=ax2+bx(a>0)经过点A和x轴正半轴上的点B,AO=BO=2,∠AOB=120°.
如图,在平面直角坐标系中,顶点为M的抛物线y=ax2+bx(a>0)经过点A和x轴正半轴上的点B,AO=BO=2,∠AOB=120°.(1)求a,b的值;
(2)连结OM,求∠AOM的大小.
分析 (1)根据AO=OB=2,∠AOB=120°,求出A点坐标,以及B点坐标,进而利用待定系数法求二次函数解析式;
(2)根据解析式求出M点坐标,再利用锐角三角函数关系求出∠FOM=30°,进而得出答案.
解答 解:(1)如图,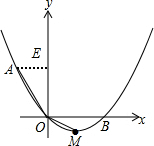
过点A作AE⊥y轴于点E,
∵AO=OB=2,∠AOB=120°,
∴∠AOE=30°,
∴AE=1,EO=$\sqrt{3}$,
∴A点坐标为:(-1,$\sqrt{3}$),B点坐标为:(2,0),
将两点代入y=ax2+bx得:
$\left\{\begin{array}{l}{a-b=\sqrt{3}}\\{4a+2b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{\sqrt{3}}{3}}\\{b=-\frac{2\sqrt{3}}{3}}\end{array}\right.$.
∴a=$\frac{\sqrt{3}}{3}$,b=-$\frac{2\sqrt{3}}{3}$;
(2)由(1)可知:抛物线的表达式为:y=$\frac{\sqrt{3}}{3}$x2-$\frac{2\sqrt{3}}{3}$x;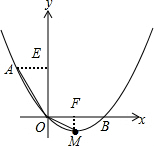
过点M作MF⊥OB于点F,
∵y=$\frac{\sqrt{3}}{3}$x2-$\frac{2\sqrt{3}}{3}$x=$\frac{\sqrt{3}}{3}$(x2-2x)=$\frac{\sqrt{3}}{3}$(x-1)2-$\frac{\sqrt{3}}{3}$,
∴M点坐标为:(1,-$\frac{\sqrt{3}}{3}$),
∴tan∠FOM=$\frac{FM}{FO}$=$\frac{\sqrt{3}}{3}$,
∴∠FOM=30°,
∴∠AOM=30°+120°=150°.
点评 此题考查二次函数的综合运用,掌握锐角三角函数、待定系数法求二次函数解析式是解决问题的关键.

 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案| A. | $\left\{\begin{array}{l}{x+2y=1}\\{3y-z=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{2x+3y=5}\\{x-y=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+y=2}\\{xy=-3}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{y=3x-2}\\{\frac{2}{x}-1=0}\end{array}\right.$ |
①等角的余角相等;
②一个角的补角一定大于这个角;
③有理数分为正数和负数;
④零是最小的正数;
⑤过直线外一点可以作一条以上的直线与已知直线平行.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | 三个点确定一个圆 | |
| B. | 同弧所对的圆周角与圆心角相等 | |
| C. | 直径是圆中最长的弦 | |
| D. | 圆是轴对称图形,不是中心对称图形 |
 如图是由几个相同的小正方体搭成的立体图形,则从它的上面看到的图形是
如图是由几个相同的小正方体搭成的立体图形,则从它的上面看到的图形是 .
.
 如图,点A的坐标是(2,1),点B的坐标是(5,1),过点A的直线l的表达式为y=2x+b,点C在直线l上运动,在直线OA上是否存在一点D,使得以A,B,C,D为顶点的四边形是平行四边形?若存在,求出点D的坐标;若不存在,请说明理由.
如图,点A的坐标是(2,1),点B的坐标是(5,1),过点A的直线l的表达式为y=2x+b,点C在直线l上运动,在直线OA上是否存在一点D,使得以A,B,C,D为顶点的四边形是平行四边形?若存在,求出点D的坐标;若不存在,请说明理由.