题目内容
 如图,AB是⊙O的直径,弦CD垂直于AB于点E,点M在⊙O上,MD恰好经过圆心O,连接MB.
如图,AB是⊙O的直径,弦CD垂直于AB于点E,点M在⊙O上,MD恰好经过圆心O,连接MB.(1)若CD=16,BE=4,求⊙O的直径;
(2)若∠B=∠D,求∠D的度数.
考点:垂径定理,勾股定理,圆周角定理
专题:计算题
分析:(1)设⊙O的半径为r,根据垂径定理,由AB⊥CD得到DE=
CD=8,在Rt△ODE中,利用勾股定理得(r-4)2+82=r2,解得r=10,所以⊙O的直径为20;
(2)由OM=OB得到∠B=∠M,根据三角形外角性质得∠DOB=∠B+∠M=2∠B,则2∠B+∠D=90°,加上∠B=∠D,所以2∠D+∠D=90°,然后解方程即可得∠D的度数.
| 1 |
| 2 |
(2)由OM=OB得到∠B=∠M,根据三角形外角性质得∠DOB=∠B+∠M=2∠B,则2∠B+∠D=90°,加上∠B=∠D,所以2∠D+∠D=90°,然后解方程即可得∠D的度数.
解答:解:(1)设⊙O的半径为r,
∵AB⊥CD,
∴CE=DE=
CD=
×16=8,
在Rt△ODE中,OE=OB-BE=r-4,OD=r,
∵OE2+DE2=OD2,
∴(r-4)2+82=r2,解得r=10,
∴⊙O的直径为20;
(2)∵OM=OB,
∴∠B=∠M,
∴∠DOB=∠B+∠M=2∠B,
∵∠DOE+∠D=90°,
∴2∠B+∠D=90°,
∵∠B=∠D,
∴2∠D+∠D=90°,
∴∠D=30°.
∵AB⊥CD,
∴CE=DE=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△ODE中,OE=OB-BE=r-4,OD=r,
∵OE2+DE2=OD2,
∴(r-4)2+82=r2,解得r=10,
∴⊙O的直径为20;
(2)∵OM=OB,
∴∠B=∠M,
∴∠DOB=∠B+∠M=2∠B,
∵∠DOE+∠D=90°,
∴2∠B+∠D=90°,
∵∠B=∠D,
∴2∠D+∠D=90°,
∴∠D=30°.
点评:本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
甲乙两人同时同地同向出发沿400米环形跑道跑步,甲的速度比乙快,当甲第二次追上乙时,甲比乙跑的路程( )
| A、一样多 | B、多800m |
| C、多400m | D、少400m |
 如图,⊙O中,若∠AOC=150°,那么∠ABC=( )
如图,⊙O中,若∠AOC=150°,那么∠ABC=( )| A、150° | B、125° |
| C、105° | D、100° |
 如图,△ABC中 AE交BC于点D,AD=4,DE=2.4,BE=6,BD:DC=5:3,则AC的长等于多少.
如图,△ABC中 AE交BC于点D,AD=4,DE=2.4,BE=6,BD:DC=5:3,则AC的长等于多少. 如图,已知AB=DC,AC=DB.求证:∠1=∠2.
如图,已知AB=DC,AC=DB.求证:∠1=∠2. 如图,△ABC是等边三角形,E为BC边上一点,将三角形ABE绕点B按顺时针方向旋转后,能与△CBD重合.若BE=3cm,则DE=
如图,△ABC是等边三角形,E为BC边上一点,将三角形ABE绕点B按顺时针方向旋转后,能与△CBD重合.若BE=3cm,则DE= 二次函数y=ax2+bx+c(a≠0)的图象如图,下列4个结论中结论正确的有
二次函数y=ax2+bx+c(a≠0)的图象如图,下列4个结论中结论正确的有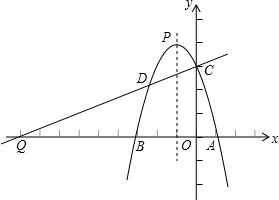 如图,已知抛物线y=ax2+bx+3与x轴交于A(1,0),B(-3,0)两点,与y轴交于点C,抛物线的顶点为P,连接AC.
如图,已知抛物线y=ax2+bx+3与x轴交于A(1,0),B(-3,0)两点,与y轴交于点C,抛物线的顶点为P,连接AC. 如图,在Rt△ABC中,∠A=90°,AB=4,AC=2,点E为AC的中点,点F在边BC上,且FE⊥BE,则CF=
如图,在Rt△ABC中,∠A=90°,AB=4,AC=2,点E为AC的中点,点F在边BC上,且FE⊥BE,则CF=