题目内容
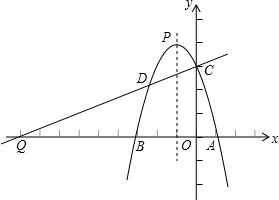 如图,已知抛物线y=ax2+bx+3与x轴交于A(1,0),B(-3,0)两点,与y轴交于点C,抛物线的顶点为P,连接AC.
如图,已知抛物线y=ax2+bx+3与x轴交于A(1,0),B(-3,0)两点,与y轴交于点C,抛物线的顶点为P,连接AC.(1)求此抛物线的解析式;
(2)在抛物线上找一点D,使得DC与AC垂直,且直线DC与x轴交于点Q,求直线DC的解析式;
(3)抛物线对称轴上是否存在一点M,使得S△MAP=2S△ACP?若存在,求出M点的坐标;若不存在,请说明理由.
考点:二次函数综合题
专题:
分析:(1)把点A(1,0),B(-3,0)两点,代入求出a和b的值,二次函数解析式即可求出;
(2)利用△QOC∽△COA,得出QO的长度,得出Q点的坐标,再求出直线QC的解析式,将两函数联立求出交点坐标即可;
(3)首先求出二次函数顶点坐标,S四边形AEPC=S四边形OEPC+S△AOC,以及S四边形AEPC=S△AEP+S△ACP=得出使得S△MAP=2S△ACP点M的坐标.
(2)利用△QOC∽△COA,得出QO的长度,得出Q点的坐标,再求出直线QC的解析式,将两函数联立求出交点坐标即可;
(3)首先求出二次函数顶点坐标,S四边形AEPC=S四边形OEPC+S△AOC,以及S四边形AEPC=S△AEP+S△ACP=得出使得S△MAP=2S△ACP点M的坐标.
解答:解:(1)∵抛物线与x轴交于A(1,0)、B(-3,0)两点,
∴
,
解得:
,
∴y=-x2-2x+3,
(2)∵点A(1,0),点C(0,3),
∴OA=1,OC=3,
∵DC⊥AC,
∴∠DCO+∠OCA=90°,
∵OC⊥x轴,
∴∠COA=∠COQ,∠OAC+∠OCA=90°,
∴∠DCO=∠OAC,
∴△QOC∽△COA,
∴
=
,
即
=
,
∴OQ=9,
又∵点Q在x轴的负半轴上,
∴Q(-9,0),
设直线QC的解析式为:y=mx+n,则
,
解之得:
,
∴直线QC的解析式为:y=
x+3,
∵点D是抛物线与直线QC的交点,
,
解之得:
或
(不合题意,应舍去),
∴点D(-
,
);
(3)如图,点M为直线x=-1上一点,连接AM,PC,PA,
设点M(-1,y),直线x=-1与x轴交于点E,
∴E(-1,0),
∵A(1,0),
∴AE=2,
∵抛物线y=-x2-2x+3的顶点为P,对称轴为x=-1,
∴P(-1,4),
∴PE=4,
则PM=|4-y|,
∵S四边形AEPC=S四边形OEPC+S△AOC,
=
×1×(3+4)+
×1×3,
=
×10,
=5,
又∵S四边形AEPC=S△AEP+S△ACP,
S△AEP=
AP•PE=
×2×4,
∴S△ACP=5-4=1,
∵S△MAP=2S△ACP,
∴
×2×|y-4|=2×1,
∴|4-y|=2,
∴y1=2,y2=6,
故抛物线的对称轴上存在点M使S△MAP=2S△ACP,
点M(-1,2)或(-1,6).
∴
|
解得:
|
∴y=-x2-2x+3,
(2)∵点A(1,0),点C(0,3),
∴OA=1,OC=3,
∵DC⊥AC,
∴∠DCO+∠OCA=90°,
∵OC⊥x轴,
∴∠COA=∠COQ,∠OAC+∠OCA=90°,
∴∠DCO=∠OAC,
∴△QOC∽△COA,
∴
| OQ |
| OC |
| OC |
| OA |
即
| OQ |
| 3 |
| 3 |
| 1 |
∴OQ=9,
又∵点Q在x轴的负半轴上,
∴Q(-9,0),
设直线QC的解析式为:y=mx+n,则
|
解之得:
|
∴直线QC的解析式为:y=
| 1 |
| 3 |
∵点D是抛物线与直线QC的交点,
|

解之得:
|
|
∴点D(-
| 7 |
| 3 |
| 20 |
| 9 |
(3)如图,点M为直线x=-1上一点,连接AM,PC,PA,
设点M(-1,y),直线x=-1与x轴交于点E,
∴E(-1,0),
∵A(1,0),
∴AE=2,
∵抛物线y=-x2-2x+3的顶点为P,对称轴为x=-1,
∴P(-1,4),
∴PE=4,
则PM=|4-y|,
∵S四边形AEPC=S四边形OEPC+S△AOC,
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=5,
又∵S四边形AEPC=S△AEP+S△ACP,
S△AEP=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△ACP=5-4=1,
∵S△MAP=2S△ACP,
∴
| 1 |
| 2 |
∴|4-y|=2,
∴y1=2,y2=6,
故抛物线的对称轴上存在点M使S△MAP=2S△ACP,
点M(-1,2)或(-1,6).
点评:此题主要考查了二次函数的综合应用,二次函数的综合应用是初中阶段的重点题型,特别注意利用数形结合是这部分考查的重点,也是难点,同学们应重点掌握.

练习册系列答案
相关题目
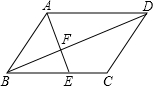 如图,?ABCD中,E是边BC上的点,AE交BD于点F,如果
如图,?ABCD中,E是边BC上的点,AE交BD于点F,如果| BE |
| BC |
| 2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若a2-b2+4b-4=a2-( ),则括号内填的代数式应为( )
| A、b2+4b-4 |
| B、b2+4b+4 |
| C、b2-4b+4 |
| D、b2-4b-4 |
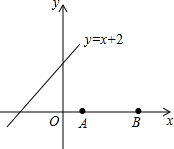 三圣乡一菜地的平面直角坐标系如图,菜地中两个灌溉喷头A(1,0),B(3,0),在菜地边缘有一水渠l:y=x+2,现要在水渠上修一水阀P,并向A,B铺设输水管,若要求P到A,B距离相等,则P的坐标为
三圣乡一菜地的平面直角坐标系如图,菜地中两个灌溉喷头A(1,0),B(3,0),在菜地边缘有一水渠l:y=x+2,现要在水渠上修一水阀P,并向A,B铺设输水管,若要求P到A,B距离相等,则P的坐标为 如图,AB是⊙O的直径,弦CD垂直于AB于点E,点M在⊙O上,MD恰好经过圆心O,连接MB.
如图,AB是⊙O的直径,弦CD垂直于AB于点E,点M在⊙O上,MD恰好经过圆心O,连接MB. 如图,在△ABC中,D为AB中点,E为AC上一点,且
如图,在△ABC中,D为AB中点,E为AC上一点,且