题目内容
 如图,在Rt△ABC中,∠A=90°,AB=4,AC=2,点E为AC的中点,点F在边BC上,且FE⊥BE,则CF=
如图,在Rt△ABC中,∠A=90°,AB=4,AC=2,点E为AC的中点,点F在边BC上,且FE⊥BE,则CF=考点:相似三角形的判定与性质,全等三角形的判定与性质
专题:
分析:过C作CD⊥EF,交EF的延长线于点D,可证明△CDE∽△EAB,利用对应边成比例可求得CD,又可证明△CDF∽△BEF,可求得CF和BF之间的关系,结合BC=BF+CF,可求出CF.
解答: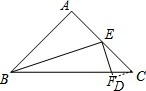 解:
解:
过C作CD⊥EF,交EF的延长线于点D,
∵BE⊥EF,且∠A=90°,
∴∠BEA+∠ABE=∠BEA+∠DEC=90°,
∴∠ABE=∠DEC,
∴△CDE∽△EAB,
∴
=
,
∵E为AC中点,AC=2,
∴AE=EC=1,且AB=4,
在Rt△ABE中可求得BE=
,
∴
=
,解得CD=
,
又CD∥BE,
∴
=
,
∴
=
,
∴BF=17CF,
在Rt△ABC中,AB=4,AC=2,可求得BC=2
,
∴18CF=2
,解得CF=
,
故答案为:
.
 解:
解:过C作CD⊥EF,交EF的延长线于点D,
∵BE⊥EF,且∠A=90°,
∴∠BEA+∠ABE=∠BEA+∠DEC=90°,
∴∠ABE=∠DEC,
∴△CDE∽△EAB,
∴
| CD |
| AE |
| EC |
| BE |
∵E为AC中点,AC=2,
∴AE=EC=1,且AB=4,
在Rt△ABE中可求得BE=
| 17 |
∴
| CD |
| 1 |
| 1 | ||
|
| 1 | ||
|
又CD∥BE,
∴
| CD |
| BE |
| CF |
| BF |
∴
| ||||
|
| CF |
| BF |
∴BF=17CF,
在Rt△ABC中,AB=4,AC=2,可求得BC=2
| 5 |
∴18CF=2
| 5 |
| ||
| 9 |
故答案为:
| ||
| 9 |
点评:本题主要考查相似三角形的判定和性质,利用条件构造三角形相似是解题的关键,注意勾股定理的应用.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
 如图,AB是⊙O的直径,弦CD垂直于AB于点E,点M在⊙O上,MD恰好经过圆心O,连接MB.
如图,AB是⊙O的直径,弦CD垂直于AB于点E,点M在⊙O上,MD恰好经过圆心O,连接MB. 如图,在△ABC中,D为AB中点,E为AC上一点,且
如图,在△ABC中,D为AB中点,E为AC上一点,且