题目内容
已知平行四边形ABCD的面积为2
,连接AC,若AC=AD=2,则平行四边形ABCD的周长是 .
| 3 |
考点:平行四边形的性质
专题:
分析:首先根据题意作出图形,然后过点A作AE⊥BC于点E,设BC=2x,AE=y,易得BC•AE=2xy=2
①,x2+y2=4②,继而求得答案.
| 3 |
解答: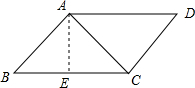 解:过点A作AE⊥BC于点E,
解:过点A作AE⊥BC于点E,
∵AB=AC,
∴BE=CE=
BC,
设BC=2x,AE=y,
∵?ABCD的面积为2
,AC=AD=2,
∴BC•AE=2xy=2
①,
在Rt△ABE中,AB2=BE2+AE2,
即x2+y2=4②,
∵AB+AC>BC,
∴2x<4,
即x<2,
由①②得:x=1,y=
,
∴BC=2,
∴?ABCD的周长为:2(AB+BC)=8.
故答案是:8.
 解:过点A作AE⊥BC于点E,
解:过点A作AE⊥BC于点E,∵AB=AC,
∴BE=CE=
| 1 |
| 2 |
设BC=2x,AE=y,
∵?ABCD的面积为2
| 3 |
∴BC•AE=2xy=2
| 3 |
在Rt△ABE中,AB2=BE2+AE2,
即x2+y2=4②,
∵AB+AC>BC,
∴2x<4,
即x<2,
由①②得:x=1,y=
| 3 |
∴BC=2,
∴?ABCD的周长为:2(AB+BC)=8.
故答案是:8.
点评:此题考查了平行四边形的性质、等腰三角形的性质以及勾股定理.此题难度适中,注意掌握方程思想与数形结合思想的应用.

练习册系列答案
相关题目
一个两位数,个位上的数是a,十位上的数b,交换个位与十位上的数字得到一个新的两位数,则这两个两位数的和是( )
| A、a+b |
| B、2(a+b) |
| C、11(a+b) |
| D、a+10b |
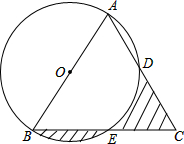 如图,在△ABC中,AB=AC=5,BC=6,以AB为直径的圆交AC于D,交BC于E,求图中阴影部分的面积.
如图,在△ABC中,AB=AC=5,BC=6,以AB为直径的圆交AC于D,交BC于E,求图中阴影部分的面积.