题目内容
已知an+1=
(n=1,3,4…2013),求当a1=1时,a1a2+a2a3+a3a4+…+a2013a2014的值.
| 1 | ||
1+
|
考点:分式的化简求值
专题:规律型
分析:已知等式整理得到关系式,把原式变形即可求出值.
解答:解:已知等式整理得:an+1=
,
当n=1时,a2=
,a3=
,a4=
,…,an=
,
则原式=
+
+
+…+
=1-
+
-
+…+
-
=1-
=
.
| an |
| an+1 |
当n=1时,a2=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n |
则原式=
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 2013×2014 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2013 |
| 1 |
| 2014 |
| 1 |
| 2014 |
| 2013 |
| 2014 |
点评:此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
 如图,在△ABC中,AB=AC,AD=DE,若∠BAD=18°,∠EDC=12°,则∠ADE=( )
如图,在△ABC中,AB=AC,AD=DE,若∠BAD=18°,∠EDC=12°,则∠ADE=( )| A、56° | B、58° |
| C、60° | D、62° |
 如图,已知点A、B、C在⊙O上,∠AOB=100°,则∠ACB的度数是( )
如图,已知点A、B、C在⊙O上,∠AOB=100°,则∠ACB的度数是( )| A、50° | B、80° |
| C、100° | D、200° |
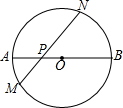 如图,在⊙O中,AB是直径,P是AB上一点,过点P作弦MN,∠NPB=45°.
如图,在⊙O中,AB是直径,P是AB上一点,过点P作弦MN,∠NPB=45°. 如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的
如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的