题目内容
3．已知对所有的实数x，|x|+$\sqrt{x-1}$≥m-|x-2|恒成立，则m可取得的最大值为2．分析 利用绝对值三角不等式求得|x|+|x-2|≥2，结合题意可得 2≥m，从而求得m的最大值．
解答 解：根据题意得：|x|+$\sqrt{x-1}$+|x-2|≥m，
∵$\sqrt{x-1}$≥0，
∴x-1≥0，
∴x≥1，
当1≤x≤2时，|x|+|x-2|的最小值为2，
∵$\sqrt{x-1}$≥0，
∴当x=1时，|x|+$\sqrt{x-1}$+|x-2的最小值为2，
∴2≥m，
∴m可取得的最大值为2；
故答案为：2．
点评 本题主要考查有理数无理数的概念与运算、绝对值以及不等式，函数的恒成立问题；解题的关键是要注意函数的恒成立与函数的最值的相互转化，体现了转化思想在解题中的应用解题中要注意函数定义域的条件．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
19．
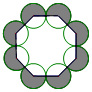如图，把八个等圆按相邻两两外切摆放，其圆心连线构成一个正八边形，设正八边形内侧八个扇形（无阴影部分）面积之和为S1，正八边形外侧八个扇形（有阴影部分）面积之和为S2，则$\frac{{S}_{1}}{{S}_{2}}$=（ ）
如图，把八个等圆按相邻两两外切摆放，其圆心连线构成一个正八边形，设正八边形内侧八个扇形（无阴影部分）面积之和为S1，正八边形外侧八个扇形（有阴影部分）面积之和为S2，则$\frac{{S}_{1}}{{S}_{2}}$=（ ）| A． | $\frac{3}{5}$ | B． | $\frac{3}{4}$ | C． | $\frac{2}{3}$ | D． | 1 |
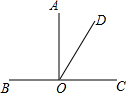如图，AO⊥BC，垂足为O，且∠COD-∠AOD=34°28′．求∠BOD的度数．
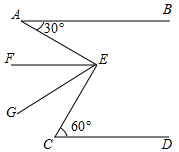如图，AB∥CD，∠BAE=30°，∠ECD=60°，EF、EG等分∠AEC，试判断EF与AB的关系并写出你的理由．
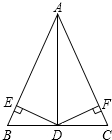如图，在△ABC中，AD是△ABC中的角平分线，BD=CD，DE⊥AB，DF⊥AC，请你在图中找出三对全等的三角形，并任选一对进行证明．