题目内容
13.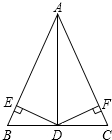 如图,在△ABC中,AD是△ABC中的角平分线,BD=CD,DE⊥AB,DF⊥AC,请你在图中找出三对全等的三角形,并任选一对进行证明.
如图,在△ABC中,AD是△ABC中的角平分线,BD=CD,DE⊥AB,DF⊥AC,请你在图中找出三对全等的三角形,并任选一对进行证明.①△ABD≌△ACD②△BDE≌△CDF③△ADE≌△ADF.
分析 根据角平分线的性质得到DE=DF,然后根据全等三角形的判定定理即可得到结论.
解答 解:①△ABD≌△ACD,②△BDE≌△CDF,③△ADE≌△ADF;
故答案为:△ABD≌△ACD,△BDE≌△CDF,△ADE≌△ADF;
∵AD是△ABC中的角平分线,DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°,DE=DF,
在Rt△AED与Rt△AFD中,$\left\{\begin{array}{l}{DE=DF}\\{AD=AD}\end{array}\right.$,
∴Rt△AED≌Rt△AFD.
点评 本题考查了全等三角形的判定、角平分线的性质,解题的关键是:(1)结合已知找出3对全等的三角形;(2)找出满足SAS的相等的边角.本题属于基础题,难度不大,解决该题型题目时,根据等腰三角形的性质找出相等的边角关系是关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
1.计算机中常用的十六进制是逢16进1的计数制,采用数字0~9和字母A~F共16个计数符号,这些符号与进制的数的对应关系如表:
例如,用十六进制表示5+A=F,3+F=12,E+D=1B,那么A+F=( )
| 16进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| 10进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| A. | 1C | B. | 1A | C. | 19 | D. | 21 |
2.某商店有2个进价不同的计算器都卖了80元,其中一个盈利60%,另一个亏本20%,在这笔买卖中,这家商店( )
| A. | 赚了10元 | B. | 赔了10元 | C. | 不赔不赚 | D. | 赚了8元 |
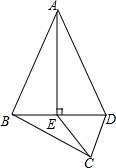 如图,四边形ABCD中,AB=AD,AE⊥BD于点E,连接CE.如果AB=13,BC=2$\sqrt{21}$,CD=4,AE=12,那么CE的长度是( )
如图,四边形ABCD中,AB=AD,AE⊥BD于点E,连接CE.如果AB=13,BC=2$\sqrt{21}$,CD=4,AE=12,那么CE的长度是( )