题目内容
12.《算法统宗》是中国古代数学名著,作者是我国明代数学家程大位.在《算法统宗》中有一道“荡秋千”的问题:“平地秋千未起,踏板一尺离地.送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.良工高士素好奇,算出索长有几?”译文:“有一架秋千,当它静止时,踏板离地1尺,将它往前推送10尺(水平距离)时,秋千的踏板就和人一样高,这个人的身高为5尺,秋千的绳索始终拉得很直,试问绳索有多长?”.
设秋千的绳索长为x尺,根据题意可列方程为x2=102+(x-4)2.
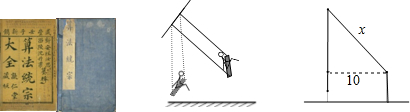
分析 设秋千的绳索长为x尺,根据题意可得AB=(x-4)尺,利用勾股定理可得x2=102+(x-4)2.
解答  解:设秋千的绳索长为x尺,根据题意可列方程为:
解:设秋千的绳索长为x尺,根据题意可列方程为:
x2=102+(x-4)2,
故答案为:x2=102+(x-4)2.
点评 此题主要考查了考差了勾股定理的应用,关键是正确理解题意,表示出AB、AC的长,掌握直角三角形中两直角边的平方和等于斜边的平方.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.下列命题是真命题的是( )
| A. | 同旁内角互补 | |
| B. | 一个角的补角大于这个角 | |
| C. | 同位角不相等,两直线不平行 | |
| D. | 如果两个角不相等,那么这两个角不是对顶角 |
7.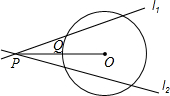 如图,点P为⊙O外一点,连结OP交⊙O于点Q,且PQ=OQ,经过点P的直线l1,l2,都与⊙O相交,则l1与l2所成的锐角α的取值范围是( )
如图,点P为⊙O外一点,连结OP交⊙O于点Q,且PQ=OQ,经过点P的直线l1,l2,都与⊙O相交,则l1与l2所成的锐角α的取值范围是( )
 如图,点P为⊙O外一点,连结OP交⊙O于点Q,且PQ=OQ,经过点P的直线l1,l2,都与⊙O相交,则l1与l2所成的锐角α的取值范围是( )
如图,点P为⊙O外一点,连结OP交⊙O于点Q,且PQ=OQ,经过点P的直线l1,l2,都与⊙O相交,则l1与l2所成的锐角α的取值范围是( )| A. | 0°<α<30° | B. | 0°<α<45° | C. | 0°<α<60° | D. | 0°<α<90° |
1.计算机中常用的十六进制是逢16进1的计数制,采用数字0~9和字母A~F共16个计数符号,这些符号与进制的数的对应关系如表:
例如,用十六进制表示5+A=F,3+F=12,E+D=1B,那么A+F=( )
| 16进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| 10进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| A. | 1C | B. | 1A | C. | 19 | D. | 21 |
2.某商店有2个进价不同的计算器都卖了80元,其中一个盈利60%,另一个亏本20%,在这笔买卖中,这家商店( )
| A. | 赚了10元 | B. | 赔了10元 | C. | 不赔不赚 | D. | 赚了8元 |
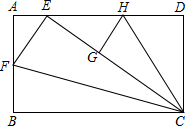 如图矩形ABCD是一张标准纸,长BC=AD=$\sqrt{2}$,AB=CD=1,把△BCF沿CF对折使点B恰好落在边AD上的点E处,再把△DCH沿CH对折使点D落在线段CE上的点G处.
如图矩形ABCD是一张标准纸,长BC=AD=$\sqrt{2}$,AB=CD=1,把△BCF沿CF对折使点B恰好落在边AD上的点E处,再把△DCH沿CH对折使点D落在线段CE上的点G处. 如图,AD=2,AB=4,∠DAB=45°,BD=BC,BD⊥BC,则AC=6.
如图,AD=2,AB=4,∠DAB=45°,BD=BC,BD⊥BC,则AC=6.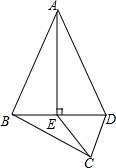 如图,四边形ABCD中,AB=AD,AE⊥BD于点E,连接CE.如果AB=13,BC=2$\sqrt{21}$,CD=4,AE=12,那么CE的长度是( )
如图,四边形ABCD中,AB=AD,AE⊥BD于点E,连接CE.如果AB=13,BC=2$\sqrt{21}$,CD=4,AE=12,那么CE的长度是( )