题目内容
14.阅读下面材料:随着人们认识的不断深入,毕达哥拉斯学派逐渐承认$\sqrt{2}$不是有理数,并给出了证明.假设是$\sqrt{2}$有理数,那么存在两个互质的正整数p,q,使得$\sqrt{2}$=$\frac{p}{q}$,于是p=$\sqrt{2}$q,两边平方得p2=2q2.因为2q2是偶数,所以p2是偶数,而只有偶数的平方才是偶数,所以p也是偶数.因此可设p=2s,代入上式,得4s2=2q2,即q2=2s2,所以q也是偶数,这样,p和q都是偶数,不互质,这与假设p,q互质矛盾,这个矛盾说明,$\sqrt{2}$不能写成分数的形式,即$\sqrt{2}$不是有理数.请你有类似的方法,证明$\root{3}{2}$不是有理数.
分析 根据题意利用反证法假设$\root{3}{2}$是有理数,进而利用假设得出矛盾,从而得出假设不成立原命题正确.
解答 解:假设$\root{3}{2}$是有理数,
则存在两个互质的正整数m,n,使得$\root{3}{2}$=$\frac{n}{m}$,
于是有2m3=n3,
∵n3是2的倍数,
∴n是2的倍数,
设n=2t(t是正整数),则n3=8t3,即8t3=2m3,
∴4t3=m3,
∴m也是2的倍数,
∴m,n都是2的倍数,不互质,与假设矛盾,
∴假设错误,
∴$\root{3}{2}$不是有理数.
点评 此题主要考查了实数的概念以及反证法的应用,正确掌握反证法的基本步骤是解题关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
4.下列式子不能因式分解的是( )
| A. | x2-4 | B. | 3x2+2x | C. | x2+25 | D. | x2-4x+4 |
19.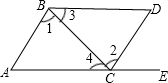 如下图所示,点E在AC的延长线上,下列条件中不能判断BD∥AC( )
如下图所示,点E在AC的延长线上,下列条件中不能判断BD∥AC( )
 如下图所示,点E在AC的延长线上,下列条件中不能判断BD∥AC( )
如下图所示,点E在AC的延长线上,下列条件中不能判断BD∥AC( )| A. | ∠3=∠4 | B. | ∠1=∠2 | C. | ∠D=∠DCE | D. | ∠D+∠ACD=180° |
6.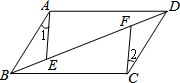 如图,平行四边形ABCD中,E,F是对角线BD上的两点,如果添加一个条件使AE∥CF,则添加的条件不能是( )
如图,平行四边形ABCD中,E,F是对角线BD上的两点,如果添加一个条件使AE∥CF,则添加的条件不能是( )
 如图,平行四边形ABCD中,E,F是对角线BD上的两点,如果添加一个条件使AE∥CF,则添加的条件不能是( )
如图,平行四边形ABCD中,E,F是对角线BD上的两点,如果添加一个条件使AE∥CF,则添加的条件不能是( )| A. | BF=DE | B. | BE=FD | C. | AE=CF | D. | ∠1=∠2 |
3.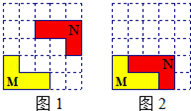 在5×5方格纸中将图①中的图形N平移后的位置如图②所示,那么下面平移中正确的是( )
在5×5方格纸中将图①中的图形N平移后的位置如图②所示,那么下面平移中正确的是( )
 在5×5方格纸中将图①中的图形N平移后的位置如图②所示,那么下面平移中正确的是( )
在5×5方格纸中将图①中的图形N平移后的位置如图②所示,那么下面平移中正确的是( )| A. | 先向下移动1格,再向左移动1格 | B. | 先向下移动1格,再向左移动2格 | ||
| C. | 先向下移动2格,再向左移动1格 | D. | 先向下移动2格,再向左移动2格 |
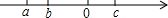 实数a,b,c在数轴上的位置如图所示,则化简$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$+$\sqrt{{c}^{2}}$-$\sqrt{{(a-c)}^{2}}$-$\sqrt{{(b+c)}^{2}}$的结果为( )
实数a,b,c在数轴上的位置如图所示,则化简$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$+$\sqrt{{c}^{2}}$-$\sqrt{{(a-c)}^{2}}$-$\sqrt{{(b+c)}^{2}}$的结果为( )