题目内容
已知抛物线y=ax2+bx-8与x轴交于A(-2,0)、B(x2,0),与y轴正半轴交于C,且S△BOC-S△AOC=4,求抛物线的解析式.
考点:抛物线与x轴的交点
专题:计算题
分析:先确定C点坐标,再利用三角形面积公式得到
•8•(-x2)-
•8•2=4,解得x2=-3,则B点坐标为(-3,0),然后利用待定系数法求抛物线的解析式.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:如图, C点坐标为(0,8),
C点坐标为(0,8),
∵A(-2,0)、B(x2,0),与y轴正半轴交于C,
∴OA=2,OB=-x2,
∵S△BOC-S△AOC=4,
∴
•8•(-x2)-
•8•2=4,解得x2=-3,
∴B点坐标为(-3,0),
把A(-2,0)、B(-3,0)代入y=ax2+bx+8得
,解得
,
∴抛物线的解析式为y=
x2+
x+8.
 C点坐标为(0,8),
C点坐标为(0,8),∵A(-2,0)、B(x2,0),与y轴正半轴交于C,
∴OA=2,OB=-x2,
∵S△BOC-S△AOC=4,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴B点坐标为(-3,0),
把A(-2,0)、B(-3,0)代入y=ax2+bx+8得
|
|
∴抛物线的解析式为y=
| 4 |
| 3 |
| 20 |
| 3 |
点评:本题考查了抛物线与x轴的交点:求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标.△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
相关题目
 如图,已知正比例函数和反比例函数的图象都经过点A(3,3).
如图,已知正比例函数和反比例函数的图象都经过点A(3,3). 已知,如图,AB为⊙O的直径,弦DC延长线上有一点P,∠PAC=∠PDA.
已知,如图,AB为⊙O的直径,弦DC延长线上有一点P,∠PAC=∠PDA.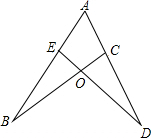 如图,已知AB=AD,BO=DO,求证:AE=AC.
如图,已知AB=AD,BO=DO,求证:AE=AC.