题目内容

3．已知一个直角三角形的两直角边之和是20cm，则这个直角三角形面积的最大值是（　　）cm2．
A．25B．50C．75D．不确定

分析 设一条直角边长为a，则另一直角边长为20-a，然后列出三角形的面积与a的函数关系式，然后利用二次函数的性质可求得三角形的最大面积．

解答 解：设一条直角边长为a，则另一直角边长为20-a．
直角三角形面积=$\frac{1}{2}a$（20-a）=$-\frac{1}{2}$a2+10a=-${\frac{1}{2}}^{\;}$（a-10）2+50．
∴三角形的面积的最大值为50．
故选：B．

点评 本题主要考查的是二次函数的最值，列出三角形的面积与a的函数关系式是解题的关键．

练习册系列答案
相关题目
13．如图，△ABC中，∠ACB=90°，D为AB中点，BC=6，CD=5，则△ABC的面积等于24．
14．如果单项式-2x4a-by3与$\frac{1}{2}$x2ya+b是同类项，这两个单项式的积是（　　）
A．x4y6B．-x2y3C．$-\frac{3}{2}$x2y3D．-x4y6
11．（1-$\frac{1}{{2}^{2}}$）（1-$\frac{1}{{3}^{2}}$）（1-$\frac{1}{{4}^{2}}$）（1-$\frac{1}{{5}^{2}}$）（1-$\frac{1}{{6}^{2}}$）（1-$\frac{1}{{7}^{2}}$）（1-$\frac{1}{{8}^{2}}$）=$\frac{9}{16}$．
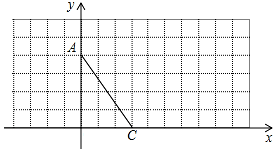18．如图，在直角坐标系中，A（0，4）、C（3，0），
（1）①画出线段AC关于y轴对称线段AB，B点的坐标为（-3，0）；
②将线段CA绕点C顺时针旋转一个角，得到对应线段CD，使得AD∥x轴，请画出线段CD；
（2）若直线y=kx平分（1）中四边形ABCD的面积，实数k的值为$\frac{4}{3}$．
8．在△ABC中，AB=AC，AD⊥BC于点D，DE∥AB交AC于点E，若∠ADE=25°，则∠BAC的度数为50°．
15．如图，抛物线y=-x2+bx+c与x轴交于A、B两点，与y轴交与点C，点O为坐标原点，点D为抛物线的顶点，点E在抛物线上，点F在x轴上，四边形OCEF为矩形，且OF=2，EF=3
（1）求抛物线的解析式并配成顶点式（要求写出过程）；
（2）求△ABD的面积；
（3）将△AOC绕点C逆时针旋转90°，点A对应点为点G，问点G是否在该抛物线上？请说明理由．
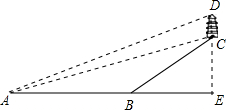12．鹅岭公园是重庆最早的私家园林，前身为礼园，是国家级AAA旅游景区，园内有一瞰胜楼，登上高楼能欣赏到重庆的优美景色，周末小嘉同学游览鹅岭公园，如图，在A点处观察到毗胜楼楼底C的仰角为12°，楼顶D的仰角为13°，BC是一斜坡，测得点B与CD之间的水平距离BE=450米．BC的坡度i=8：15，则测得水平距离AE=1200m，BC的坡度i=8：15，则瞰胜楼的高度CD为（　　）米．（参考数据：tan12°=0.2，tan13°=0.23）
A．34B．35C．36D．37
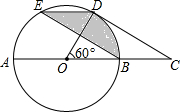13．如图，在⊙O中，AB是直径，点D是⊙O上一点且∠BOD=60°，过点D作⊙O的切线CD交AB的延长线于点C，E为$\widehat{AD}$的中点，连接DE，EB．
（1）求证：四边形BCDE是平行四边形；
（2）已知图中阴影部分面积为12π，求⊙O的半径r．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网