题目内容
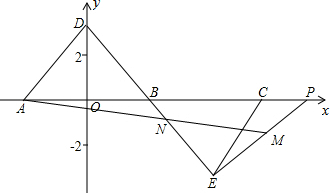
如图,平面直角坐标系中,已知A(-2,0),B(2,0),C(6,0),D为y轴正半轴上一点,且∠ODB=30°,延长DB至E,使BE=BD.P为x轴正半轴上一动点(P在C点右边),M在EP上,且∠EMA=60°,AM交BE于N.
(1)求证:BE=BC;
(2)求证:∠ANB=∠EPC;
(3)当P点运动时,求BP-BN的值.
(1)求证:BE=BC;
(2)求证:∠ANB=∠EPC;
(3)当P点运动时,求BP-BN的值.

考点:全等三角形的判定与性质,坐标与图形性质,等边三角形的判定与性质
专题:
分析:(1)根据点A、B的坐标求出AD=BD,根据直角三角形两锐角互余求出∠ABD=60°,然后判断出△ABD是等边三角形,根据等边三角形的性质可得BD=AB=4,再求出BC=4,从而得到BC=BD,然后等量代换即可得证;
(2)根据三角形的一个外角等于与它不相邻的两个内角的和可得∠BAN+∠ANB=∠ABD=60°,∠BAN+∠EPC=∠EMA=60°,即可得证;
(3)求出△BCE是等边三角形,根据等边三角形的性质可得BC=CE,然后求出AB=CE,再求出∠ABN=∠ECP=120°,然后利用“角角边”证明△ABN和△ECP全等,根据全等三角形对应边相等BN=CP,再根据BP-CP=BC等量代换即可得解.
(2)根据三角形的一个外角等于与它不相邻的两个内角的和可得∠BAN+∠ANB=∠ABD=60°,∠BAN+∠EPC=∠EMA=60°,即可得证;
(3)求出△BCE是等边三角形,根据等边三角形的性质可得BC=CE,然后求出AB=CE,再求出∠ABN=∠ECP=120°,然后利用“角角边”证明△ABN和△ECP全等,根据全等三角形对应边相等BN=CP,再根据BP-CP=BC等量代换即可得解.
解答:(1)证明:∵A(-2,0),B(2,0),
∴AD=BD,AB=4,
∵∠ODB=30°,
∴∠ABD=90°-30°=60°,
∴△ABD是等边三角形,
∴BD=AB=4,
∵B(2,0),C(6,0),
∴BC=6-2=4,
∴BC=BD,
又∵BE=BD,
∴BE=BC;
(2)证明:由三角形的外角性质得,∠BAN+∠ANB=∠ABD=60°,
∠BAN+∠EPC=∠EMA=60°,
所以,∠ANB=∠EPC;
(3)解:∵BE=BD=BC,∠CBE=∠ABD=60°,
∴△BCE是等边三角形,
∴BC=CE,
∵AB=BC=4,
∴AB=CE,
∵∠ABC=∠BCE=60°,
∴∠ABN=∠ECP=120°,
在△ABN和△ECP中,
,
∴△ABN≌△ECP(AAS),
∴BN=CP,
∵BP-CP=BC,
∴BP-BN=BC=4,
故BP-BN的值为4,与点P的位置无关.
∴AD=BD,AB=4,
∵∠ODB=30°,
∴∠ABD=90°-30°=60°,
∴△ABD是等边三角形,
∴BD=AB=4,
∵B(2,0),C(6,0),
∴BC=6-2=4,
∴BC=BD,
又∵BE=BD,
∴BE=BC;
(2)证明:由三角形的外角性质得,∠BAN+∠ANB=∠ABD=60°,
∠BAN+∠EPC=∠EMA=60°,
所以,∠ANB=∠EPC;
(3)解:∵BE=BD=BC,∠CBE=∠ABD=60°,
∴△BCE是等边三角形,
∴BC=CE,
∵AB=BC=4,
∴AB=CE,
∵∠ABC=∠BCE=60°,
∴∠ABN=∠ECP=120°,
在△ABN和△ECP中,
|
∴△ABN≌△ECP(AAS),
∴BN=CP,
∵BP-CP=BC,
∴BP-BN=BC=4,
故BP-BN的值为4,与点P的位置无关.
点评:本题考查了全等三角形的判定与性质,坐标与图形性质,等边三角形的判定与性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记各性质并准确识图是解题的关键,难点在于根据边的长度相等得到相等的边.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
如图,用火柴棒按如图的方式搭三角表,搭一个三角形需3根火柴棒,如图甲,搭两个三角形需5根火柴棒,如图乙,搭三个三角形需7根火柴棒,如图丙,那么按此规律搭下去,搭10个三角形需要多少根火柴棒( )


| A、30 | B、21 |
| C、119 | D、111 |
 如图,在△ABD中,AC⊥BD,点C是BD的中点,则下列结论错误的是( )
如图,在△ABD中,AC⊥BD,点C是BD的中点,则下列结论错误的是( )| A、AB=AD |
| B、AB=BD |
| C、∠B=∠D |
| D、AC平分∠BAD |
 如图,梯形ABCD中AD∥BC,∠B=90,P为DC上一点,PE⊥AB、PF⊥BC垂足分别为E、F,AD=1,AB=2,BC=5,BF=x,矩形EBFP面积为y,求y与x之间的函数关系式.
如图,梯形ABCD中AD∥BC,∠B=90,P为DC上一点,PE⊥AB、PF⊥BC垂足分别为E、F,AD=1,AB=2,BC=5,BF=x,矩形EBFP面积为y,求y与x之间的函数关系式.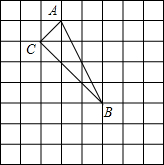 每个小正方形的边长为1.
每个小正方形的边长为1.