题目内容
5. 如图,直线y=2x+3与坐标轴交于A、B两点,点P在直线y=x上,且△ABP角平分线的交点正好在y轴上,求P点坐标.
如图,直线y=2x+3与坐标轴交于A、B两点,点P在直线y=x上,且△ABP角平分线的交点正好在y轴上,求P点坐标.
分析 根据题意可求得点A和点B的坐标,然后根据点P在直线y=x上,且△ABP角平分线的交点正好在y轴上,从而可以求得点P的坐标.
解答  解:如右图所示,
解:如右图所示,
∵点P在在直线y=x上,且△ABP角平分线的交点正好在y轴上,
∴∠ABO=∠OBP,
∵直线y=2x+3与坐标轴交于A、B两点,
当x=0时,y=-1.5,当y=0时,y=3,
∴点A的坐标为(-1.5,0),点B的坐标为:(0,3),
∴tan∠ABO=$\frac{1.5}{3}=\frac{1}{2}$,
设点P的坐标为(a,a),作PC⊥y轴于点C,
∴BC=3-a,PC=a,
∴$\frac{a}{3-a}=\frac{1}{2}$,
解得,a=1,
∴点P的坐标为(1,1).
点评 本题考查一次函数图象上点的坐标特征,解答本题的关键是明确题意,找出所求问题需要的需要的条件,作出合适的辅助线,利用数形结合的思想解答.

练习册系列答案
相关题目
13.已知A,B两点分别在反比例函数y=$\frac{3m}{x}$(m≠0)和y=$\frac{2m-5}{x}$(m≠$\frac{5}{2}$)的图象上,若点A与点B关于x轴对称,则m的值为1.
15.下列计算正确的是( )
| A. | 3x4-x2=3x2 | B. | (-2ab3)2•a=4a3b6 | C. | 8a6÷2a3=4a2 | D. | (a-2)2=a2-4 |
 如图,平面直角坐标系中,已知直线y=x上一点P(2,2)C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B,直线AB与直线y=x交于点A,且BD=2AD,连接CD,直线CD与直线y=x交于点Q.
如图,平面直角坐标系中,已知直线y=x上一点P(2,2)C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B,直线AB与直线y=x交于点A,且BD=2AD,连接CD,直线CD与直线y=x交于点Q.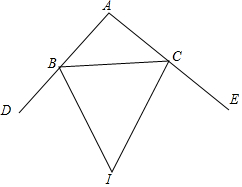 如图,BI,CI分别平分△ABC的外角∠DBC和∠ECB,
如图,BI,CI分别平分△ABC的外角∠DBC和∠ECB,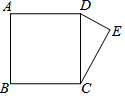 如图,正方形ABCD的边长为13,以CD为斜边向外作Rt△CDE.若点A到CE的距离为17,则CE=12或5.
如图,正方形ABCD的边长为13,以CD为斜边向外作Rt△CDE.若点A到CE的距离为17,则CE=12或5.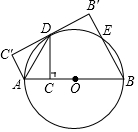 如图,AB是⊙O的直径,点C为AB上一点,作CD⊥AB交⊙O于D,连接AD,将△ACD沿AD翻折至△AC′D.
如图,AB是⊙O的直径,点C为AB上一点,作CD⊥AB交⊙O于D,连接AD,将△ACD沿AD翻折至△AC′D.

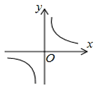
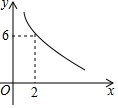 平行四边形ABCD中,AB⊥AC,∠B=45°.若平行四边形ABCD的一边长x与这条边上的高为y满足的反比例函数关系如图所示,则平行四边形ABCD的周长为4($\sqrt{3}$+$\sqrt{6}$).
平行四边形ABCD中,AB⊥AC,∠B=45°.若平行四边形ABCD的一边长x与这条边上的高为y满足的反比例函数关系如图所示,则平行四边形ABCD的周长为4($\sqrt{3}$+$\sqrt{6}$).