题目内容
13.已知A,B两点分别在反比例函数y=$\frac{3m}{x}$(m≠0)和y=$\frac{2m-5}{x}$(m≠$\frac{5}{2}$)的图象上,若点A与点B关于x轴对称,则m的值为1.分析 设A(a,b),则B(a,-b),将它们的坐标分别代入各自所在的函数解析式,通过方程来求m的值.
解答 解:设A(a,b),则B(a,-b),
依题意得:$\left\{\begin{array}{l}{b=\frac{3m}{a}}\\{-b=\frac{2m-5}{a}}\end{array}\right.$,
所以$\frac{3m+2m-5}{a}$=0,即5m-5=0,
解得m=1.
故答案是:1.
点评 本题考查了反比例函数图象上点的坐标特征,关于x轴,y轴对称的点的坐标.根据题意得$\frac{3m+2m-5}{a}$=0,即5m-5=0是解题的难点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8. 如图,在平面直角坐标系中,平行四边形OABC的顶点A的坐标为(-4,0),顶点B在第二象限,∠BAO=60°,BC交y轴于点D,DB:DC=3:1.若函数y=$\frac{k}{x}$(k>0,x>0)的图象经过点C,则k的值为( )
如图,在平面直角坐标系中,平行四边形OABC的顶点A的坐标为(-4,0),顶点B在第二象限,∠BAO=60°,BC交y轴于点D,DB:DC=3:1.若函数y=$\frac{k}{x}$(k>0,x>0)的图象经过点C,则k的值为( )
 如图,在平面直角坐标系中,平行四边形OABC的顶点A的坐标为(-4,0),顶点B在第二象限,∠BAO=60°,BC交y轴于点D,DB:DC=3:1.若函数y=$\frac{k}{x}$(k>0,x>0)的图象经过点C,则k的值为( )
如图,在平面直角坐标系中,平行四边形OABC的顶点A的坐标为(-4,0),顶点B在第二象限,∠BAO=60°,BC交y轴于点D,DB:DC=3:1.若函数y=$\frac{k}{x}$(k>0,x>0)的图象经过点C,则k的值为( )| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $\sqrt{3}$ |
18.下列计算正确的是( )
| A. | (-3x)3=-27x3 | B. | (x-2)2=x4 | C. | x2÷x-2=x2 | D. | x-1•x-2=x2 |
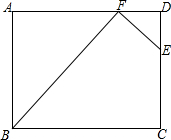 如图,ABCD是长方形,AB=6,BC=8,CE=4,四边形BCEF的面积是30,那么三角形DEF的面积是多少?
如图,ABCD是长方形,AB=6,BC=8,CE=4,四边形BCEF的面积是30,那么三角形DEF的面积是多少? 如图,直线y=2x+3与坐标轴交于A、B两点,点P在直线y=x上,且△ABP角平分线的交点正好在y轴上,求P点坐标.
如图,直线y=2x+3与坐标轴交于A、B两点,点P在直线y=x上,且△ABP角平分线的交点正好在y轴上,求P点坐标.