题目内容
17.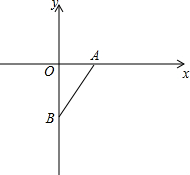 如图,已知平面直角坐标系中有点A(3,0)和点B(0,-4),在x轴上存在一点C,使得△ABC为等腰三角形,则C坐标为(-3,0)、(8,0)、(-2,0)、(-$\frac{7}{6}$,0).
如图,已知平面直角坐标系中有点A(3,0)和点B(0,-4),在x轴上存在一点C,使得△ABC为等腰三角形,则C坐标为(-3,0)、(8,0)、(-2,0)、(-$\frac{7}{6}$,0).
分析 分为三种情况:①AB=AC,②AC=BC,③AB=BC,画出图形,即可得出答案.
解答  解:∵A(3,0)和点B(0,-4),
解:∵A(3,0)和点B(0,-4),
∴AO=3,OB=4,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=5,
如图:
①以A为圆心,以AB为半径作弧,交x轴于AC1=AC4=5此时两点C1(-2,0),C4(8,0);
②当AC=BC时,此时点C在AB的垂直平分线上,C3(-$\frac{7}{6}$,0);
③以B为圆心,以AB为半径作弧,交x轴于C2,此时AB=BC,点C2(-3,0);
综上所述点C的坐标为:(-3,0)、(8,0)、(-2,0)、(-$\frac{7}{6}$,0).
故答案为:(-3,0)、(8,0)、(-2,0)、(-$\frac{7}{6}$,0).
点评 本题考查了等腰三角形的判定,坐标与图形性质的应用,用了分类讨论思想.

练习册系列答案
相关题目
8. 如图,过y轴上任意一点P,作x轴的平行线,分别与反比例函数y=-$\frac{4}{x}$和y=$\frac{2}{x}$的图象交于A点和B点,若C为x轴上任意一点,连接AC,BC,则△ABC的面积为( )
如图,过y轴上任意一点P,作x轴的平行线,分别与反比例函数y=-$\frac{4}{x}$和y=$\frac{2}{x}$的图象交于A点和B点,若C为x轴上任意一点,连接AC,BC,则△ABC的面积为( )
 如图,过y轴上任意一点P,作x轴的平行线,分别与反比例函数y=-$\frac{4}{x}$和y=$\frac{2}{x}$的图象交于A点和B点,若C为x轴上任意一点,连接AC,BC,则△ABC的面积为( )
如图,过y轴上任意一点P,作x轴的平行线,分别与反比例函数y=-$\frac{4}{x}$和y=$\frac{2}{x}$的图象交于A点和B点,若C为x轴上任意一点,连接AC,BC,则△ABC的面积为( )| A. | 3 | B. | 4 | C. | 6 | D. | 5 |
2.十二五”规划纲要指出,我国将在今后5年内新建3600万套保障性住房,使保障房覆盖率达到20%.3600万这个数用科学记数法可表示为( )
| A. | 36×102 | B. | 3.6×103 | C. | 3.6×107 | D. | 3.6×108 |
 如图,有足够多的正方形(A型和B型)和长方形(C型)卡片,利用这些卡片可以进行因式分解,如对多项式2a2+3ab+b2进行因式分解.
如图,有足够多的正方形(A型和B型)和长方形(C型)卡片,利用这些卡片可以进行因式分解,如对多项式2a2+3ab+b2进行因式分解. 如图,△ABC中,∠BAC=90°,AC=2AB,D为AC的中点,AF⊥BC于F,DG⊥AC交AF的延长线于G,BD交AG于H.
如图,△ABC中,∠BAC=90°,AC=2AB,D为AC的中点,AF⊥BC于F,DG⊥AC交AF的延长线于G,BD交AG于H. 某文具店到批发市场选购A、B两种文具,批发价分别为14元/个、10元/个.若该店零售A、B两种文具的每天销量y(个)与零售价x(元/个)都是一次函数y=kx+20的关系,如图所示.
某文具店到批发市场选购A、B两种文具,批发价分别为14元/个、10元/个.若该店零售A、B两种文具的每天销量y(个)与零售价x(元/个)都是一次函数y=kx+20的关系,如图所示. 如图,直线l过点A(4,0)和点B(0,4),它与二次函数y=ax2+2的图象交于点P,若△AOP的面积为$\frac{9}{2}$.求二次函数的表达式.
如图,直线l过点A(4,0)和点B(0,4),它与二次函数y=ax2+2的图象交于点P,若△AOP的面积为$\frac{9}{2}$.求二次函数的表达式.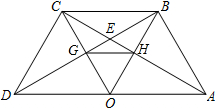 如图,点O为线段AD上的中点,分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形OCD,连接AC,BD交于点E,AC,BD分别与OB,OC相交于点H,G,连接BC.
如图,点O为线段AD上的中点,分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形OCD,连接AC,BD交于点E,AC,BD分别与OB,OC相交于点H,G,连接BC.