题目内容
5. 如图,△ABC中,∠BAC=90°,AC=2AB,D为AC的中点,AF⊥BC于F,DG⊥AC交AF的延长线于G,BD交AG于H.
如图,△ABC中,∠BAC=90°,AC=2AB,D为AC的中点,AF⊥BC于F,DG⊥AC交AF的延长线于G,BD交AG于H.(1)求证:CE=AH.
(2)求证:BC=CE+HG.
分析 (1)先证明AB=CD=AD,∠CDE=∠ABH,根据ASA证明△CED≌△AHB即可;
(2)易证∠GDA=∠CAB=90°,∠C=∠G,根据ASA证明△CAB≌△GDA即可.
解答 证明:(1)∵AC=2AB,D为AC的中点,
∴AB=CD=AD,
∵∠BAC=90°,
∴∠BAH+∠CAF=90°,
∵AF⊥BC,
∴∠C+∠CAF=90°,
∴∠BAH=∠C,
∵∠BDE=90°,
∴∠CDE+∠BDA=90°,
又∵∠BDA+∠ABH=90°,
∴∠CDE=∠ABH,
在△CED和△AHB中,
$\left\{\begin{array}{l}{∠CDE=∠ABH}\\{AB=CD}\\{∠BAH=∠C}\end{array}\right.$,
∴△CED≌△AHB(ASA),
∴CE=AH;
(2)∵DG⊥AC,
∴∠GDA=∠CAB=90°,∠C=∠G,
在△CAB和△GDA中,
$\left\{\begin{array}{l}{∠C=∠G}\\{AB=AD}\\{∠GDA=∠CAB}\end{array}\right.$,
∴△CAB≌△GDA(ASA),
∴BC=AG=AH+HG,
∵CE=AH,
∴BC=CE+HG.
点评 本题主要考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解决问题的关键.

练习册系列答案
相关题目
 甲、乙两车同时以一定的速度从A城出发前往B城,行驶途中甲接到电话,立刻以同样的速度返回A城,然后提高速度前往B城,结果比乙车早到1小时,设甲、乙两车从A城出发的时间为t(小时),距离A城距离为y km,如图所示,则A,B两城距离是300km.
甲、乙两车同时以一定的速度从A城出发前往B城,行驶途中甲接到电话,立刻以同样的速度返回A城,然后提高速度前往B城,结果比乙车早到1小时,设甲、乙两车从A城出发的时间为t(小时),距离A城距离为y km,如图所示,则A,B两城距离是300km.
 如图是一个水平放置的油管的截面图,其中油面的宽AB为16cm,油面的深度CD=4cm,求油管截面圆的半径.
如图是一个水平放置的油管的截面图,其中油面的宽AB为16cm,油面的深度CD=4cm,求油管截面圆的半径.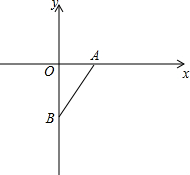 如图,已知平面直角坐标系中有点A(3,0)和点B(0,-4),在x轴上存在一点C,使得△ABC为等腰三角形,则C坐标为(-3,0)、(8,0)、(-2,0)、(-$\frac{7}{6}$,0).
如图,已知平面直角坐标系中有点A(3,0)和点B(0,-4),在x轴上存在一点C,使得△ABC为等腰三角形,则C坐标为(-3,0)、(8,0)、(-2,0)、(-$\frac{7}{6}$,0). 如图,已知△ABC中,AB=AC=10厘米,BC=8厘米,点D为AB的中点.
如图,已知△ABC中,AB=AC=10厘米,BC=8厘米,点D为AB的中点.