题目内容
3．
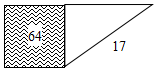如图，阴影部分是一个面积为64的正方形，以它的一边为直角边作斜边长为17的直角三角形，这个直角三角形的另一条直角边长为（ ）| A． | 9 | B． | 15 | C． | 47 | D． | 9 |
分析 先求出AB的长，再根据勾股定理即可得出结论．
解答 
解：∵阴影部分是一个面积为64的正方形，
∴AB=8．
∵BC=17，
∴AC=$\sqrt{B{C}^{2}-A{B}^{2}}$=$\sqrt{1{7}^{2}-{8}^{2}}$=15．
故选B．
点评 本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
练习册系列答案
相关题目
如图所示，在△ABC中，AD平分∠BAC，DE⊥AB于点E，DF⊥AC于点F，试说明AD与EF的关系．
11．在平面直角坐标系中，点P的坐标为（0，2），点M的坐标为（m，-$\frac{3}{4}$m-3）（其中m为实数），当PM的长最小时，m的值为（ ）
| A． | -$\frac{12}{5}$ | B． | -$\frac{17}{5}$ | C． | -3 | D． | -4 |
18．
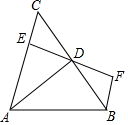如图，AD是△ABC的角平分线，DE⊥AC，垂足为E，BF∥AC交ED的延长线于点F，若BC恰好平分∠ABF，AE=2EC，给出下列四个结论：①DE=DF；②DB=DC；③AD⊥BC；④AB=3BF，其中正确的结论共有（ ）
如图，AD是△ABC的角平分线，DE⊥AC，垂足为E，BF∥AC交ED的延长线于点F，若BC恰好平分∠ABF，AE=2EC，给出下列四个结论：①DE=DF；②DB=DC；③AD⊥BC；④AB=3BF，其中正确的结论共有（ ）| A． | ①②③ | B． | ①③④ | C． | ②③ | D． | ①②③④ |
12．
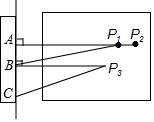如图是一跳远运动员跳落沙坑时留下的痕迹，则表示该运动员成绩的是（ ）
如图是一跳远运动员跳落沙坑时留下的痕迹，则表示该运动员成绩的是（ ）| A． | 线段AP1的长 | B． | 线段AP2的长 | C． | 线段BP3的长 | D． | 线段CP3的长 |