题目内容
18.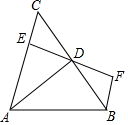 如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2EC,给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AB=3BF,其中正确的结论共有( )
如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2EC,给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AB=3BF,其中正确的结论共有( )| A. | ①②③ | B. | ①③④ | C. | ②③ | D. | ①②③④ |
分析 据等腰三角形的性质三线合一得到BD=CD,AD⊥BC,故②③正确;通过△CDE≌△DBF,得到DE=DF,CE=BF,故①④正确.
解答 解:∵BF∥AC,
∴∠C=∠CBF,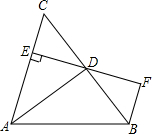
∵BC平分∠ABF,
∴∠ABC=∠CBF,
∴∠C=∠ABC,
∴AB=AC,
∵AD是△ABC的角平分线,
∴BD=CD,AD⊥BC,故②③正确,
在△CDE与△DBF中,
$\left\{\begin{array}{l}{∠C=∠CBF}\\{CD=BD}\\{∠EDC=∠BDF}\end{array}\right.$,
∴△CDE≌△DBF,
∴DE=DF,CE=BF,故①正确;
∵AE=2EC,
∴AC=3EC=3BF,故④正确.
故选D.
点评 本题考查了全等三角形的判定和性质,等腰三角形的性质,平行线的性质,掌握等腰三角形的性质三线合一是解题的关键.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
 如图,在△ABC中,AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,AB=6,AC=4,若S△ABD=9,求S△ACD.
如图,在△ABC中,AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,AB=6,AC=4,若S△ABD=9,求S△ACD.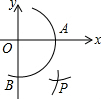 如图,在平面直角坐标系中,以点O为圆心,适当的长为半径画弧,交x轴于点A,交y轴于点B,再分别以点A,B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧在第四象限交于点P.若点P的坐标为(2a,a-9),则a的值为3.
如图,在平面直角坐标系中,以点O为圆心,适当的长为半径画弧,交x轴于点A,交y轴于点B,再分别以点A,B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧在第四象限交于点P.若点P的坐标为(2a,a-9),则a的值为3.

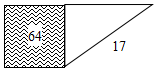 如图,阴影部分是一个面积为64的正方形,以它的一边为直角边作斜边长为17的直角三角形,这个直角三角形的另一条直角边长为( )
如图,阴影部分是一个面积为64的正方形,以它的一边为直角边作斜边长为17的直角三角形,这个直角三角形的另一条直角边长为( ) 如图,BD=CD,DE⊥AB,DF⊥AC,DE=DF,∠A=90°,试说明:AB=AC.
如图,BD=CD,DE⊥AB,DF⊥AC,DE=DF,∠A=90°,试说明:AB=AC.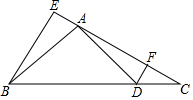 如图,在△ABC中,AB=AC,过A作AD⊥AB交BC于点D,过B作BE⊥AC,交CA延长线于点E,过D作DF⊥AC,垂足为F.若EF=3$\sqrt{3}$.BC=6$\sqrt{2}$.则tan∠C=$\frac{\sqrt{2}}{2}$.
如图,在△ABC中,AB=AC,过A作AD⊥AB交BC于点D,过B作BE⊥AC,交CA延长线于点E,过D作DF⊥AC,垂足为F.若EF=3$\sqrt{3}$.BC=6$\sqrt{2}$.则tan∠C=$\frac{\sqrt{2}}{2}$.