题目内容

11．在平面直角坐标系中，点P的坐标为（0，2），点M的坐标为（m，-$\frac{3}{4}$m-3）（其中m为实数），当PM的长最小时，m的值为（　　）
A．-$\frac{12}{5}$B．-$\frac{17}{5}$C．-3D．-4

分析 由两点间的距离公式可得出PM2关于m的二次函数关系式，利用配方法结合二次函数的性质即可得出当PM取最小值时m的值．

解答 解：由两点间的距离公式可知：
PM2=m2+（-$\frac{3}{4}$m-5）2=$\frac{25}{16}$m2+$\frac{15}{2}$m+25=$\frac{25}{16}$（m2+$\frac{24}{5}$m）+25=$\frac{25}{16}$（m+$\frac{12}{5}$）2+16，
∵$\frac{25}{16}$＞0，
∴当m=-$\frac{12}{5}$时，PM2最小．
故选A．

点评 本题考查了两点间的距离公式以及二次函数的性质，解题的关键是找出PM2关于m的二次函数关系式．

练习册系列答案
相关题目
20．如图，A，B，C是⊙O上的三个点，若∠AOC=100°，则∠ABC等于130°．
2．在平面直角坐标系xOy中，已知点A（t，0），B（t+2，0），M（3，4）．以点M为圆心，1为半径画圆．点P是圆上的动点，则△ABP的面积的最小值和最大值依次为3，5．
19．如图，点（3，m）为直线AB上的点．求该点的坐标．
6．问题提出：我们知道，等式具有性质：（1）等式两边同时加或减同一个代数式，所得结果仍是等式；（2）等式两边同时乘同一个数或除以同一个不为0的数，所得结果仍是等式．那么任意 一个三阶幻方是否也有类似的性质？
问题探究：为了探究上述问题，我们不妨从简单的三阶幻方①入手；
探究一
如图②，九个数2，3，4，5，6，7，8，9，10已填到方格中，显然每行、每列、每条对角线上的三个数之和都相等，构成了一个三阶幻方②，所以构成三阶幻方①的九个数同时加1，所得到的九个数仍可构成一个三阶幻方．
如图③，九个数-2，-1，0，1，2，3，4，5，6已填到方格中，显然每行、每列、每条对角线上的三个数之和都相等，构成了一个三阶幻方③，所以构成三阶幻方①的九个数同时减3，所得到的九个数仍可构成一个三阶幻方．
     请把九个数0.5，1.5，2.5，3.5，4.5，5.5，6.5，7.5，8.5填到图④的方格中，使得每行、每列、每条对角线上的三个数之和都相等，构成了一个三阶幻方④，所以构成三阶幻方①的九个数同时减0.5，所得到的九个数仍可构成一个三阶幻方．
1．根据探究一可得任意三阶幻方的性质（1）：构成三阶幻方的九个数，每个数同时加或减同一个数，所得到的九个数仍能构成三阶幻方．
探究二：
如图⑤，九个数3，6，9，12，15，18，21，24，27已填到方格中，显然每行、每列、每条对角线上的三个数之和都相等，构成了一个三阶幻方⑤．所以构成三阶幻方①的九个数同时乘3，所得到的九个数仍可构成一个三阶幻方．
如图⑥，九个数0.5，1，1.5，2，2.5，3，3.5，4，4.5已填到方格中，显然每行、每列、每条对角线上的三个数之和都相等，构成了一个三阶幻方⑥．所以构成三阶幻方①的九个数同时除以2，所得到的九个数仍可构成一个三阶幻方．
     请把九个数-2，-4，-6，-8，-10，-12，-14，-16，-18填到图⑦的方格中，使得每行、每列、每条对角线上的三个数之和都相等，构成了一个三阶幻方⑦．所以构成三阶幻方①的九个数同时乘-2，所得到的九个数仍可构成一个三阶幻方．
2．根据探究二可得任意三阶幻方的性质（2）：构成三阶幻方的九个数，每个数同时乘同一个数或除以同一个不为0的数，所得到的九个数仍能构成三阶幻方．．
性质应用：
3，5，7，9，11，13，15，17，19这九个数能否构成三阶幻方？请用三阶幻方的性质进行说明．
16．对于平面直角坐标系中的线段PQ和点M，在△MPQ中，当PQ边上的高为2时，称M为PQ的“等高点”，称此时MP+MQ为PQ的“等高距离”．己知P（1，2），Q（4，2）．
（1）在A（0，3），B（-1，-1），C（-1，0），D（$\frac{13}{3}$，4）中，PQ的“等高点”是C、D；
（2）若M′（5，4）为PQ的“等高点”，则此时PQ的“等高距离”是3$\sqrt{5}$；
（3）若M（m，4）为PQ的“等高点”，求PQ的“等高距离”的最小值及此时m的值．
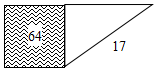3．如图，阴影部分是一个面积为64的正方形，以它的一边为直角边作斜边长为17的直角三角形，这个直角三角形的另一条直角边长为（　　）
A．9B．15C．47D．9
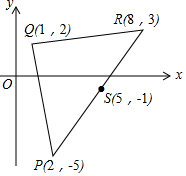20．图中的P（2，-5），Q（1，2）和R（8，3）是一个三角形的顶点
（a）证明△PQR是一个等腰三角形．
（b）若S（5，-1）是PR上的一点，证明QS⊥PR．
（c）由此，或用其他方法，求△PQR的面积．
1．计算：
（1）$\sqrt{64}$+$\frac{\root{3}{-27}}{2}$-$\sqrt{（-7）^{2}}$
（2）解方程$\left\{\begin{array}{l}{x-2y=5}\\{3x+y=1}\end{array}\right.$
（3）解方程$\left\{\begin{array}{l}{4b+a=15}\\{3a-4b=-3}\end{array}\right.$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网