题目内容

证明：四边形内角和为360°．
考点：多边形内角与外角,三角形内角和定理
专题：证明题
分析：要证明四边形的内角和问题，三角形的内角和已知是180度，这样就可以把四边形的问题转化为三角形的问题．转化的方法是作出四边形一条对角线，就转化为两个三角形．
解答：证明：如图：

连接一条对角线，把四边形分成两个三角形，
一个三角形内角和为180°，所以两个三角形的内角和为360°，
四边形的内角和是360．
点评：本题考查了多边形的内角和，关键是连接一条对角线，把四边形分成两个三角形．
练习册系列答案
相关题目
如图，在平行四边形ABCD中，A1、A2、A3、A4和C1、C2、C3、C4分别为AB和CD的五等分点，点B1、B2和D1、D2分别是BC和DA的三等分点，已知四边形ABCD的面积为15，则平行四边形A4B2C4D2（阴影部分）的面积为（　　）
A、6B、8C、9D、10
如图，在Rt△ABC中，∠ABC=90°，D、E在AC上，且AB=AD，CB=CE．求∠EBD的度数．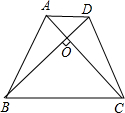
如图所示，已知在等腰梯形ABCD中，AD∥BC，AC⊥BD，AB+BC=18，求梯形ABCD的高．
小明有一副三角尺和一个量角器（如图所示）．

（1）小明的这三件文具中，可以看做是轴对称图形的是
 
（填字母代号）；
（2）请用这三个图形中的两个拼成一个轴对称图案，画出草图（须画出四种）；
（3）小红也有同样的一副三角尺和一个量角器．若他们分别从自己这三件文具中随机取出一件，则可以拼成一个轴对称图案的概率是多少？（请画树状图或列表计算）
解答下列各题：
（1）解不等式组
x-3
2
+3≥x
1-3(x-1)＜8-x
，并把其解集在数轴上表示出来．
（2）将4个数a，b，c，d排成2行、2列，记成
aamp;b
camp;d
，定义
aamp;b
camp;d
=ad-bc，上述记号就叫做2阶行列式．若
x+1amp;x-1
1-xamp;x+1
=6，求x的值．
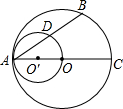如图，OA是⊙O的半径，AB是⊙O的弦，以OA为直径的圆与AB相交于点D，
（1）说明：BD与AD的关系；
（2）若点D在圆上运动（与A不重合），则（1）中求得的AD与BD的大小关系是否保持不变？为什么？
某农户1997年承包荒山若干亩，投资7800元改造后种果树2000棵，其成活率为90%．在今年（注：今年指2000年）夏季全部结果时，随意摘下10棵果树的水果，称得重量如下：（单位：千克）
8，9，12，13，8，9，11，10，12，8
（1）根据样本平均数估计该农户今年水果的总产量是多少？
（2）此水果在市场每千克售1.3元，在水果园每千克售1.1元，该农户用农用车将水果拉到市场出售，平均每天出售1000千克，需8人帮助，每人每天付工资25元．若两种出售方式都在相同的时间内售完全部水果，选择哪种出售方式合理？为什么？
（3）该农户加强果园管理，力争到2002年三年合计纯收入达到57000元，求2001年、2002年平均每年的增长率是多少？（纯收入=总收入-总支出）
已知在一个三角形中，若第一个内角的度数是第二个内角的度数的
3
2
，第三个内角的度数比这两个内角的度数的和大20°，求这三个内角的度数．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网